撰稿 / 張鳳吟 (科學推展中心特約編輯)
反問題(inverse problem)是一個倒果為因的計算過程，從已知的觀測結果推斷產生它的未知原因。由於反問題可以告訴我們無法直接觀察的未知參數，它在數學及科學應用上都是非常重要的研究課題，其中，科學應用範例包括電阻抗成像，其利用介質邊界測量到的電壓或電流重構介質內部的電導率(condutivity)，這問題又稱為Calderὸn問題[註1]。不過應用上的反問題通常是非線性與非良質的(ill-posed)，意指不滿足數學家Hadamard所提出的三個適定性條件：解存在、唯一、並隨著初始條件連續地改變，因此反問題以純數觀點也是個相當挑戰的問題。
偏微分方程(partial differential equations，PDEs)可粗分為橢圓、拋物、雙曲三種類型，典型相應的方程式分別為 Laplace 方程、波方程、熱方程(不考慮常數項)：
Laplace方程(橢圓)：\(u_{x1x1}+u_{x2x2}=0\)
波方程(拋物)：\(u_{x1x1}-u_{x2x2}=0\)
熱方程(雙曲)：\(u_{x2}-u_{x1x1}=0\)
偏微分方程的反問題，是利用PDEs的部分解重構原方程式的係數、邊界條件、初始條件、domain的形狀或甚至奇異點等，在過去幾十年，非線性PDEs的反問題受到了很大的關注。研究非線性PDEs反問題的方法主要仰賴適當的線性化技巧，最早是由數學家V. Isakov在1993年所開創，他證明半線性拋物方程式相應的Dirichlet-to-Neumann(DN)映射的線性化，與相關線性化方程式的DN映射一致。對於半線性橢圓方程式\(∆u+a(x,u)=0\)，在過去已有人研究2維與\(\geq\)3維，從邊界上\(u\)值決定係數\(a\left(x,u\right)\)的反問題；除此之外，反邊界值問題也有相關研究。
哥倫布計畫與國際年輕傑出學者研究計畫得主、
他們考慮下列擴散半線性橢圓方程的Dirichlet 問題。設\(\Omega\subset\mathbb{R}^n\)為具光滑邊界的有界封閉區間(bounded connected domain)、
為其內部具光滑邊界的空穴(cavity)，方程式可表示為：
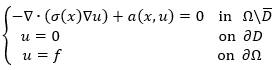(Eqn.1)
其中\(\sigma\left(x\right)\)、\(a\left(x,u\right)\)分別代表擴散與係數項；當\(D=\emptyset\)(即方程式為完全數據)，Eqn. 1變為：
(Eqn.2)
團隊假設擴散項\(\sigma\)與低階係數項\(a\)為分段實解析函數(piecewise real-analytic，即冪級數)，先證明存在一個\(\varepsilon>0\)，當\(\varepsilon\)夠小時上述兩個方程式結果為局部適定(local well-posedness)，接著定義從Dirichlet邊界(邊界值為u在邊界上的測量值)到Neumann邊界(邊界值為沿邊界法線方向的變化)的相應映射，其中\(\nu\)為邊界單位法線向量，\(\Gamma\subseteq\partial\Omega\)為開放邊界部分：
(1) (部分)DN算子：\(\Lambda_{\sigma,a}^\Gamma:N_\varepsilon\rightarrow H^{-\frac{1}{2}}(\Gamma)\), \(\Lambda_{\sigma,a}^\Gamma\left(f\right)=\sigma\partial_\nu\left.u_f\right|_\Gamma\)，
\(u_f\)為Eqn.2的唯一解。
(2) DN算子：\(\Lambda_{\sigma,a,D}^\Gamma:N_\varepsilon\rightarrow H^{-\frac{1}{2}}(\Gamma)\), \(\Lambda_{\sigma,a,D}^\Gamma\left(f\right)=\sigma\partial_\nu\left.u_f\right|_\Gamma\)，
\(u_f\)為Eqn.1的唯一解。
「同步恢復反問題」便是探討以下兩個問題：
(1) 我們可以透過部分測量\(\Lambda_{\sigma,a}^\Gamma\)來同步獲得\(\sigma\)和\(a\)嗎？
(2) 我們可以透過部分測量\(\Lambda_{\sigma,a,D}^\Gamma\)來同步獲得\(\sigma\)、\(a\)與D嗎？
林奕亘助理教授團隊在這篇最新的工作中給出肯定的答案。他們採用高階線性化的方法，引進特別的參數將半線性橢圓方程縮減為不同的線性橢圓方程式。而在兩年前，林奕亘助理教授與芬蘭合作團隊為第一次利用高階線性化的方法來處理相關半線性的橢圓問題[2]。線性化後，不同於其他團隊利用複雜的幾何光學解，他們利用單調性(monotonicity)方法與局部化勢(localized potentials)來處理所得到的線性化橢圓方程。他們證明，兩個封閉區間\(\Omega\)\\(\bar{D}\)與\(\Omega\)\\(\bar{\widetilde{D}}\)內兩組係數(\(\sigma\),a)與(\(\widetilde{\sigma}\),\(\widetilde{a}\))，在\(\varepsilon>0\)足夠小時，假設對所有\(f\in N_\varepsilon\)，\(\Lambda_{\sigma,a,D}^\Gamma\left(f\right)\)= \(\Lambda_{\widetilde{\sigma},\widetilde{a},\widetilde{D}}^\Gamma\left(f\right)\)，則\(\sigma=\widetilde{\sigma}\)、\(a=\widetilde{a}\)、與\(D=\widetilde{D}\)。林奕亘助理教授表示，即使在完全數據的例子(即\(\Gamma=\partial\Omega\))，這個理論仍是一項新的結果。這定理包含D或\(\widetilde{D}\)其中一個為空集合的情形，因此，知道DN算子就能同步決定擴散(\(\sigma\))、吸收係數(\(a\))以及空穴的形狀(D)。
註1：關於電阻抗成像的反問題，可以參考科學推展中心台大數學系王振男教授的研究介紹： https://spec.ntu.edu.tw/20221220-research-math/
參考文獻
[1] Bastian Harrach and Yi-Hsuan Lin, Simultaneous recovery of piecewise analytic coefficients in a semilinear elliptic equation, Nonlinear Analysis 228 (2023) 113188
[2] Matti Lassas, Tony Liimatainen, Yi-Hsuan Lin and Mikko Salo, Inverse problems for elliptic equations with power type nonlinearities, J. Math. Pures Appl., Vol. 145 (2021), 44-82.
