志書的關卡

遊戲開始時，志書（張豐豪飾）面對的關卡，要求他在不碰到繩結的狀況下，判斷哪一個繩結可以被拉成一個單純的圓環。這跟數學有啥關係？

有關！因為真的有一個專門研究繩結的數學：紐結理論。

題目內容

以上哪一個繩結能夠被拉成一個單純的圓環？

在紐結理論中，有一個叫做亞歷山大多項式的玩意，它有一個重要的性質：

不論你如何拉扯繩結
其對應的亞歷山大多項式不會變
(至多只會被同乘±t^k)

這讓亞歷山大多項式像是紐結的DNA：不管你如何喬裝易容，這個DNA都不會變。而因為單純圓環的亞歷山大多項式是1，因此一個紐結，只要它算出來的亞歷山大多項式不只一項，那它無論如何都無法被拉成圓環。

所以問題就只剩下亞歷山大多項式怎麼算了！這邊以最左邊的紐結舉例。
第一步：先把整個結看成一條單行道，並把每一個交叉點編號。
第二步：有幾個交叉點，就列出一個幾乘幾的方陣，並把每一排每一列都依據交叉點的名稱編號。
第三步：現在對於每一個橫行，檢查其對應的交叉點：

舉例來說，對於這個結，A箭頭指的那個交叉點，上方道路是到D箭頭，而此時左邊會是A，右邊會是B，因此A的那一行會填成上面所示的樣子。
第四步：把整個方陣都填完後，把最後一行跟最後一列刪掉，然後算它的行列式值，最後得到的就是亞歷山大多項式。

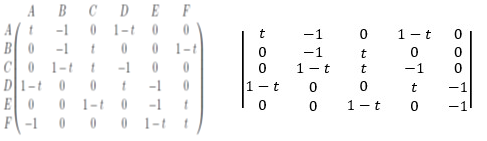
依照以上四步驟，三個紐結的方陣以及亞歷山大多項式如下：

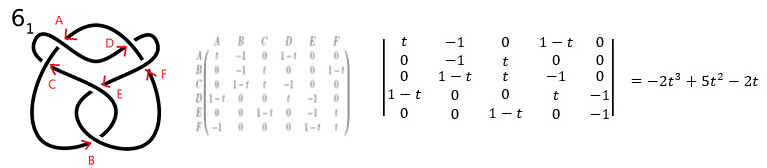
前兩個結的亞歷山大多項式都多於1項，所以它不可能被拉成單純的圓環，故只有最後一個結是有可能的。

您可能會問：為啥要研究這個，直接拉一拉，看看能不能把繩結拉開不就行了？關於這個問題，首先，就算知道一個結能被還原成圓環，要找出還原的確切步驟，其實也不是一個容易的問題。大家可以自己試試看，上面那個結要如何還原成圓環。

此外，紐結理論的應用可不只在單純的「繩結」上唷！有興趣的朋友，可以參考這個連結。