撰稿 / 張鳳吟 (科學推展中心特約編輯)
圖1、超音速流通過圓錐所形成的衝擊波。(改編自 Supersonic Flow and Shock Waves , Richard Courant, p.407 )
超音速流(supersonic flow)遇見障礙物，如圓錐狀的物體，是空氣動力學(aerodynamics)一個重要的基本問題。空氣動力學研究固體影響下的空氣運動，其中物體與空氣的速度常以無因次的馬赫數 M (Mach number，M=u/c ，u 為物體或空氣速度，c 為音速)來表示，M>1 稱為超音速，M<1 稱為次音速。當M接近1，介於臨界馬赫數(通常約0.8)與一個更高的值(通常為1.2)之間，物體周圍會同時存在超音速與次音速的氣流，這個區間稱為跨音速(transonic)。跨音速區間會有衝擊波(shock wave)產生，在這個區間飛行的飛機容易失去平衡，原因是衝擊波增加了阻力，並導致機體周圍氣流的不對稱及不穩定。為了飛航安全，航太工程師努力研究機形與機翼的設計來減弱跨音速區間衝擊波的影響。
圓錐在空氣動力學是非常重要的形狀，以超音速飛行的飛機(如協和號[註1])、子彈或導彈等等，鼻錐常近似於圓錐狀。當超音速流通過攻角為0的圓錐體，這個問題便為軸對稱。設圓錐為無窮大，頂點位於原點，超音速流受圓錐影響在尖端形成衝擊波(波兩側物理性質不連續的改變)，對於小的圓錐張角，衝擊波為conical shock，與圓錐同頂點；對於大的圓錐張角，衝擊波為bow shock，與圓錐分離(如圖1)。
將圓錐對稱軸設為x軸，y為到x軸的垂直距離，u、v分別為相應的流速分量，當流體等熵、穩定，可用可壓縮尤拉方程式來表示：
\(\frac{\partial}{\partial x}\rho u+\frac{\partial}{\partial y}\rho v=-\frac{1}{y}\rho v,\)
\(\frac{\partial}{\partial x}\left(\rho u^2+P\right)+\frac{\partial}{\partial y}\rho uv=-\frac{1}{y}\rho uv,\)
\(\frac{\partial}{\partial x}\rho uv+\frac{\partial}{\partial y}\left(\rho v^2+P\right)=-\frac{1}{y}\rho v^2\)
其中 \(\rho\) 為空氣密度，氣壓\(P\left(\rho\right)=\rho^\gamma,\gamma>1\)。這是一個初始值問題，德國航太科學家Busemann最早在1929年提出理論解，他將通過衝擊波的流體速度作為初始條件，以圖形方法來建構錐形流(conical flow)的自相似解(self-similar solution)，錐形流的特點是所有流體性質在沿著通過圓錐頂點的射線上為常數。幾年後，1933年Taylor與Maccoll以球座標系統來討論這問題，設初始值在圓錐表面並首次發表其數值解，所計算的圓錐表面壓力與高速風洞實驗的觀測結果相當一致[註2]。
成大數學系連文璟副教授專長為偏微分方程，她與研究團隊近期研究超音速流繞錐的問題[1]。在圓錐張角\(\theta_b\)不大，衝擊波依附在圓錐頂點的情形下，團隊考慮球座標的尤拉系統，藉由解為自相似錐形流的假設，將2階的Taylor-Maccoll方程式重新整理成1階的無因次非線性常微分方程(ODE)組：
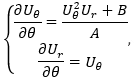
其中\(A=-U_\theta^2+\frac{\gamma-1}{2}(1-U_r^2-U_\theta^2)\)、\(B=\frac{\gamma-1}{2}\left(1-U_r^2-U_\theta^2\right)(2U_r+U_\theta\mathrm{cot\ }\theta)\)，無因次速度\(U_r\)、\(U_\theta\)分別為速度的徑向與法線方向分量對Bernoulli定律最大理論速度的歸一化。初始值設在圓錐上，對解進行積分至滿足衝擊波的Rankine-Hugoniot條件。根據過去研究數值解的結果，解會是超音速或跨音速，為此，連教授團隊關注這兩種模式之間的轉變，以及平滑跨音速流解的存在。多維空間的跨音速流是相當重要及挑戰的問題，過去已有一些相關研究，如Chen與Fang(2009)考慮跨音速衝擊波的穩定性問題等。
給定入射流速的範圍\(U_0\in(\mu,1)\)，
為音速，團隊設定圓錐上平行圓錐的初始流速為1馬赫，持續積分到解曲線(solution curve)與shock polar相交，此時得到的相應角度為\(\theta_S\)。團隊應用ODE系統的基本理論與技術估計，建構出超音速流的解。進一步假設初始流速稍低於1馬赫\((U_\ast\left(\theta_b\right)=(0,\mu-\epsilon_\ast))\)，團隊利用Gronwall不等式的分析，揭露圓錐與衝擊波之間存在超音速至次音速轉變的現象。團隊證明，不管圓錐張角\(\theta_b\)多小，只要適當選取入射流速 \(U_0\)，永遠存在平滑跨音速流的解，當正確選取\(U_0\)，\(\theta_S\)相等於滿足Rankine-Hugoniot條件的衝擊波角度 \(\beta\)。圖2為 \(\theta_b=30°\) 的數值解結果，其中 \(U_0\)=0.95，\(\gamma\)=1.4，\(U_1\)與\(U_\ast\)分別為超音速與跨音速的解，右圖為紅色區塊的放大。圖3為\(\beta-\theta_S-U_0\)關係的數值解，當\(U_0~0.6\)，\({\ \theta}_S=\beta\)。
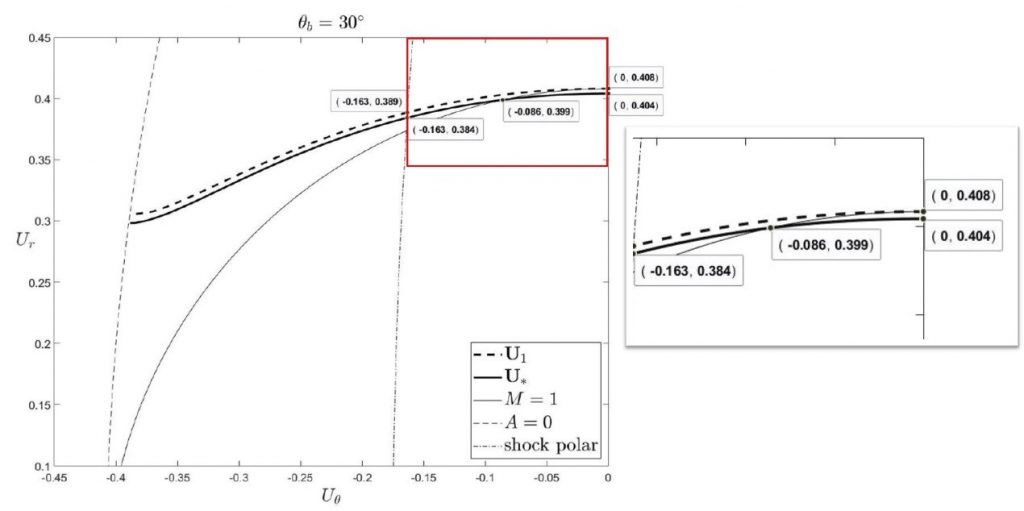
圖2、圓錐張角\(\theta_b=30° \)的數值結果，右圖為紅色區塊的放大圖，不同角度的結果類似。
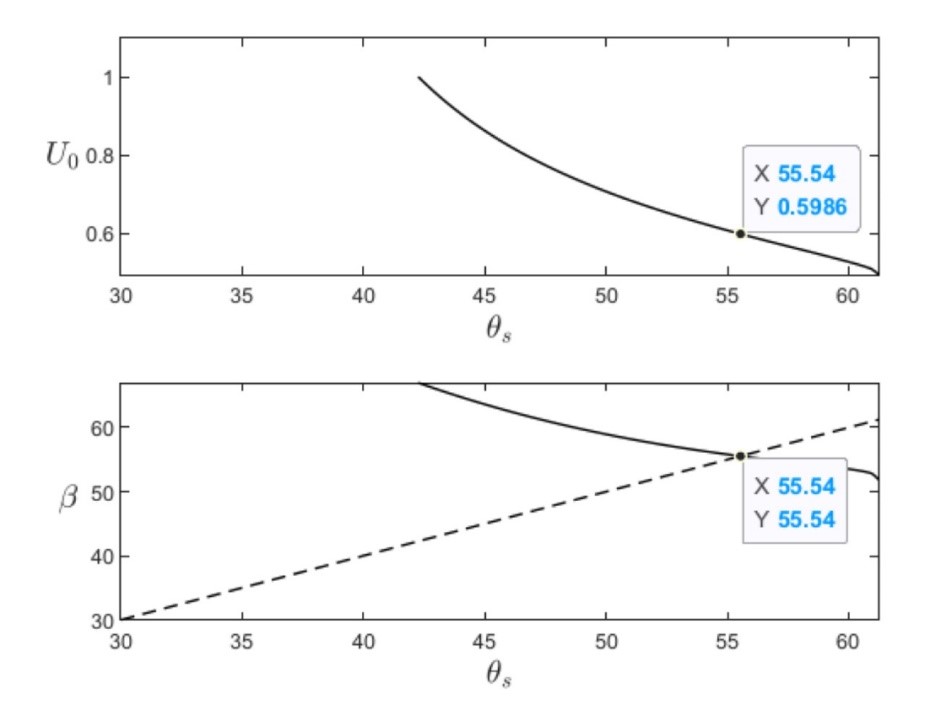
圖3、\(\beta-\theta_S-U_0\)關係的數值結果。
註1：協和號已於2002年退役。
註2：有關compressible flow理論之發展，A. Busemann和G.I. Taylor是很重要的兩位學者。可參見： “Modern Compressible Flow, with Historical Perspective” by John D. Anderson, PP 349-354, 426-427.
參考文獻
[1] Wen Ching Lien, Yu-Yu Liu, Chen Chang Peng, “Smooth Transonic Flows Around Cones”, Networks and Heterogeneous Media, Vol. 17, No. 6, December 2022, pp. 827–845
