撰稿 / 張鳳吟 (科學推展中心特約編輯)
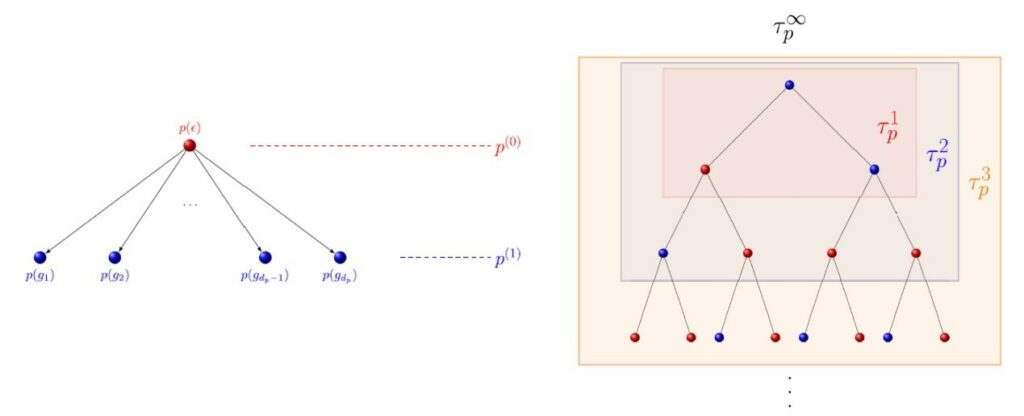
圖1. 1-spread 拓樸模型,左圖為1-generation的模式,右圖為延伸至無窮大的Induced spread pattern。
2019年的新冠肺炎(Covid-19)爆發,使得流行病傳播在近年又成為熱門的主題,為了控制疫情,科學家們發展各種數學模型來預測疫情的走向,以制定有效措施防止疫情的擴散。許多模型將個體(individuals)分成數種類型――例如susceptible(S)-infected(I)-recovered(R)模型――來表示擴散模式(pattern),有效於研究各類型個體數量及比例的動力學,以期對疾病傳播有更好的概念。
政大應用數學系洪芷漪副教授與班榮超教授等人組成合作團隊,以不同的方式,從置換動態系統(substitution dynamical system)與分支過程(branching processes) 的角度提出「決定性」的(deterministic)拓樸擴散模型與「隨機性」的(random)隨機擴散模型,這兩類系統的優點是可以透過其\(\xi\)-矩陣與後代期望值矩陣(offspring mean matrix)來表徵其傳播行為。同時這些模型將個體依擴散病毒的模式分類,擴散模式受過去m單位時間內(或generation)個體的型態組成之影響,反映接觸周圍具傳染力個體的更實際情況。當\(\xi\)-矩陣與後代期望值矩陣為primitive(即非負,非週期且不可約),團隊檢驗模型的長期行為,證明擴散率可預測並與矩陣最大固有值(eigenvalue)及相應的固有向量(eigenvector)有關[1]。
凍結型態(frozen type)的擴散模型
在大流行期間,疾病的防治措施如隔離、戴口罩等,能夠有效降低病毒的傳播,建立於先前的工作,洪芷漪團隊提出了凍結型態(frozen type)的拓樸與隨機模型[2],當稱一個型態(type)被「凍結」時,意味著個體只產生一個相同型態的個體,而該型態無法再進一步傳播,因此改變了整體病毒傳播的模式。型態的凍結可代表一些個體接受流行病控制的強迫措施(例如:隔離),具凍結型態的模型可描述實施控制手段後擴散模式之變化。
(1) 凍結型態1-spread拓樸模型:
圖1為1-spread拓樸模型(m=1),從1-模式(左圖)出發經由取代前一個generation的pattern延伸至無窮大的pattern,相應的取代圖標示為\(\xi\),相關\(\xi\)-矩陣 \(≔[O(ξ_a\)\(_i)]\),其中\(a_i\)為個體型態,\(O(ξ_a\)\(_i)\)為\(\xi(a_i)\)中出現的\(a_i\)數目。
當其中一個型態發生凍結,該型態個體只能產生一個相同型態的個體,擴散模型如圖2所示,
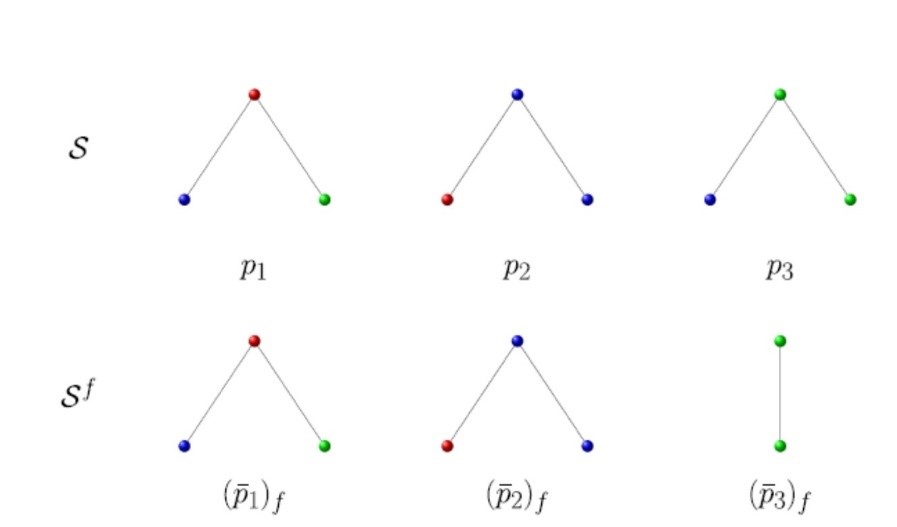
圖2. 三型態擴散模型的範例,下圖為凍結後的模式。
(2) 凍結形態隨機模型:
設一個群體由K種不同型態的個體組成,\(\mathbf{Z}_n=(Z_{n,1},Z_{n,2},\ldots,Z_{n,K})\)為n時間後的群體向量,\(Z_{n,i}\)為型態\(a_i\)的個體數,假設個體遵循機率分布\(\left\{p^{\left(i\right)}(\bullet)\right\}_{i=1}^K\)獨立於其它個體產生後代,其中\(p^{\left(j\right)}(j_1,j_2,…,j_K)\)為型態\(a_i\)個體產生個\(j_1\)型態\(a_1\)小孩、\(j_2\)個型態\(a_2\)小孩等等的機率,\(\left\{\mathbf{Z}_n\right\}_{n>0}\)稱為 K-型態分支過程,而產生不同型態後代數的期望值\(m_{i,j}=E\left(Z_{1,j}\middle|\mathbf{Z}_0=\mathrm{e}_\mathrm{i}\right)\),矩陣
\(\mathbf{M}_0\equiv\left[m_{i,j}\right]=\left[\begin{matrix}m_{11}&m_{12}&\ldots&m_{1K}\\m_{21}&m_{22}&\ldots&m_{2K}\\\vdots&&&\vdots\\m_{K1}&m_{K2}&\ldots&m_{KK}\\\end{matrix}\right]\)
稱為後代期望值矩陣。古典理論說明,當branching過程為non-singular,\(\mathbf{M}_0\)為primitive、最大固有特徵值\(\rho\left(\mathbf{M}_0\right)>1\),族群個數向量收斂\(\lim\limits_{n\rightarrow\infty}\)\({\frac{\mathbf{Z}_n}{\rho\left(\mathbf{M}_0\right)^n}\mathbf{v}_{\mathbf{M}_0}W}\),其中\(\mathbf{v}_{\mathbf{M}_0}\)為\(\rho\left(\mathbf{M}_0\right)\)相關的歸一化左固有向量,W為隨機變數。在凍結的系統,考慮型態\(a_K\)被凍結(即在流行病防治中被隔離),以機率為1只產生”1”個同型態孩子,凍結型態的後代期望值矩陣\(\mathbf{M}\)表示為
\(\mathbf{M}\equiv\left[m_{ji}^\ast\right]=\left[\begin{matrix}m_{11}&\ldots&m_{1K-1}&0\\m_{21}&\ldots&m_{2K-1}&0\\\vdots&\ldots&\vdots&\vdots\\m_{K1}&\ldots&m_{KK-1}&1\\\end{matrix}\right]\)
廣義化方法處理凍結型態擴散模型
然而在凍結系統裡,\(\xi\)-矩陣與後代期望值矩陣不必然是primitive的,因此不能直接應用古典理論的Ferron-Frobenius定理來預測擴散率。團隊建立一個新演算法,能夠以廣義的方式「明確」計算出兩者模型的擴散率,並將擴散率與兩者矩陣的固有向量連結起來,此成果發表於《Chaos》期刊[3]。具體來說,團隊(1)證明\(\xi\)-矩陣存在限制性的擴散率,並決定當\(\xi\)-矩陣可分解為primitive成分與不可約成分時,擴散率何時為正;(2)將primitive的後代期望值矩陣的古典結果延伸到凍結形態的隨機模型,團隊證明族群大小的幾何增長,其顯示型態組成的極限與矩陣最大固有值相關的右固有向量成正比,並找出擴散率。團隊進行數值計算來佐證所提出的理論,圖3、圖4分別為凍結型態拓樸模型與隨機模型群體大小與群體組成比例隨時間演變的結果,團隊揭露族群大小呈現指數型增長,族群的組成為漸進週期性。
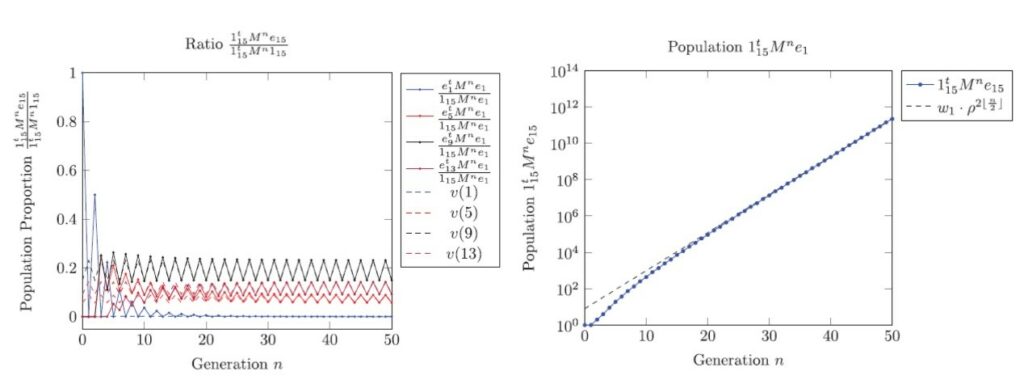
圖3. 凍結型態拓樸擴散模型的數值結果,左圖為群體比例隨時間的演變,右圖為群體大小的演變。
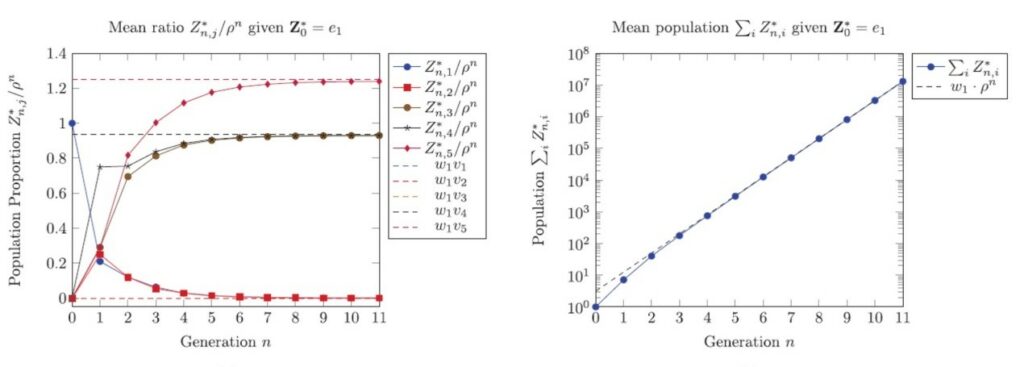
圖4. 凍結型態隨機擴散模型的數值結果,左圖為群體比例隨時間的演變,右圖為群體大小的演變。
參考文獻
[1] J.-C. Ban, J.-I. Hong, and Y.-L. Wu, “Mathematical analysis of topological and random m-order spread models,” J. Math. Biol. 86(3), 40 (2023).
[2] J.-C. Ban, J.-I. Hong, and Y.-L. Wu, “Spread rates of spread models with frozen symbols,” Chaos 32(10), 103113 (2023).
[3] J.-C. Ban, J.-I. Hong, C.-Y. Tsai, and Y.-L. Wu, ‘Topological and random spread models with frozen symbols, ‘ Chaos, 33(6), 063144 (2023).