撰稿 / 張鳳吟 (科學推展中心特約編輯)、王琪仁 (國立中正大學數學系副教授)
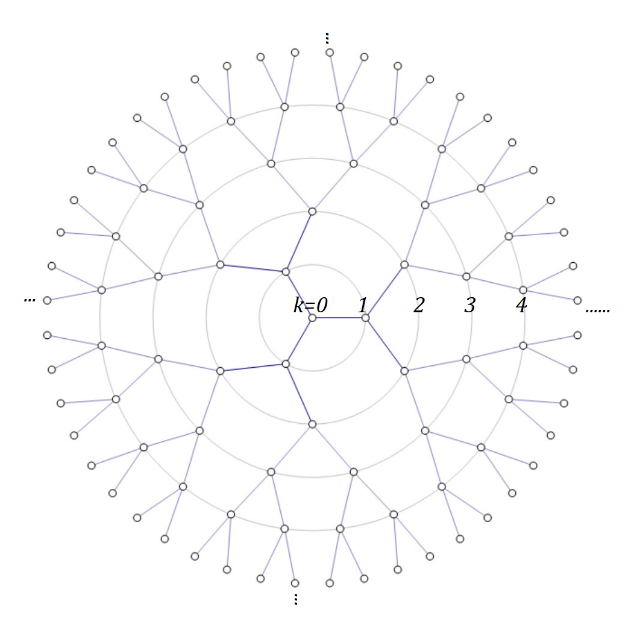
圖1. 配位數(相鄰點個數)z=3的Bethe網格示意圖。網格中每一點皆有3個相鄰點,各層所對應的環以k=0,1,2,…標示。
您是否在煮開水時曾看過,在臨界溫度時,水壺底部接近熱源的液態水變成了氣態水蒸氣泡泡向上浮出?水蒸氣在溫度較低的水壺內蓋形成了液態水滴。此時溫度稍增一點會有較多液態水轉為氣態水蒸氣泡泡,溫度稍降一點會有較多水蒸氣凝結成水滴。這類氣態與液態同時存在的兩相共存現象,是甫獲2022吳大猷先生紀念獎的國立中正大學數學系王琪仁副教授及愛荷華州立大學的美國物理學會會士James Evans教授於能源部Ames實驗室的研究團隊,長期關心的主題之一。
Schlögl模型是物理學家Friedrich Schlögl(1917-2011)用以描述非平衡相變的化學反應現象,其模型考慮了粒子生成與粒子消散兩種化學反應[1]。當粒子擴散伴隨著發生時,Schlögl第二模型能展現出兩相共存的現象。其模型亦可應用在各式動態系統上,例如:化學反應、空間流行病、社群網絡的傳播等。Bethe網格是一種特殊的無窮樹狀圖,由物理學家Hans Bethe(1906-2005)提出。
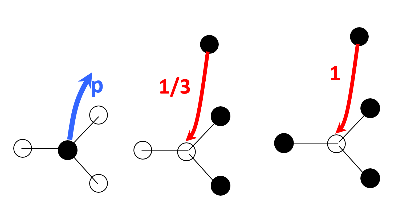
圖2. 當相鄰點個數為3時,粒子反應示意圖。(藍)粒子消散速率p。(紅)當有兩個相鄰粒子時,在中心空位點的粒子生成率為1/3;當有三個相鄰粒子時,在中心空位點的生成率為1。
研究團隊過去幾年在直角座標系中以Schlögl第二模型探索兩相共存區中的成核現象成果豐碩[2,3]。在2021年的文章中將其應用到Bethe網格上[4]。隨機動態系統在規律週期無窮網格上的行為,通常可由有限網格加上週期性邊界條件,以動態蒙地卡羅(kinetic Monte Carlo,KMC)模擬來推測。然而在Bethe網格中該週期性邊界條件使得問題複雜許多。
研究團隊比較不同邊界條件並利用改良的模擬方法,試圖尋找其模擬結果最接近無窮網格結果的有限週期邊界條件。在配位數z=3的Bethe網格上,預測出當粒子消散速率p超過大約0.053時,系統會朝全空態的不連續相變。此結果發表在美國物理學會出版的《物理評論E》期刊[4]。
參考文獻
[1] “Chemical Reaction Models for Non-Equilibrium Phase Transitions”, F. Schlögl, Physik 253, 147-161. (1972)
[2] “Schloegl’s second model for autocatalysis with particle diffusion: Lattice-gas realization exhibiting generic two-phase coexistence”, X. Guo, D.-J. Liu, and J. W. Evans. Chem. Phys. 130, 074106. (2009)
[3] “Extended Families of Critical and Stationary Droplets for Non-Equilibrium Phase Transitions in Spatially-Discrete Bistable Systems”, C.-J. Wang, D.-J. Liu, and J. W. Evans. Rev. E 101, 022803. (2020)
[4] “Phase transitions in Schloegl’s second model for autocatalysis on a Bethe lattice”, D.-J. Liu, C.-J. Wang, and J. W. Evans, Phys. Rev. E 104, 014135. (2021)