撰稿 / 何郁庭 (科學推展中心特約編輯)
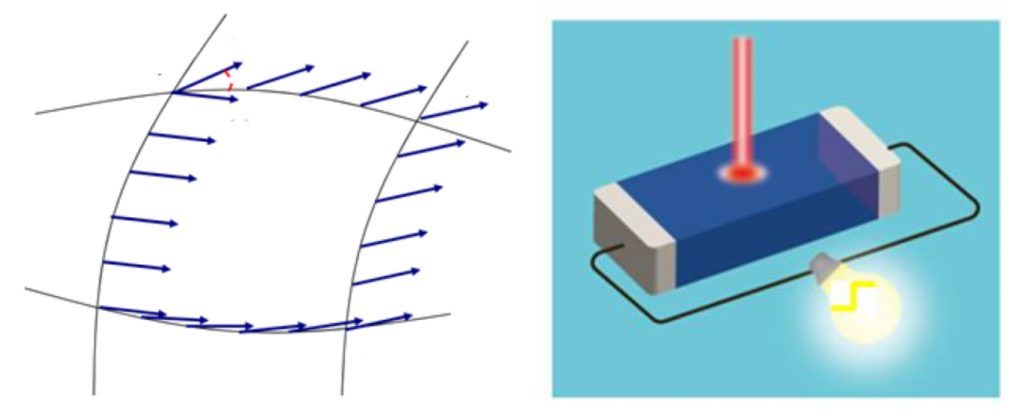
電子態的幾何結構(量子幾何),是近年來理解電子系統對靜態電磁場響應的基礎,臺大物理系郭光宇教授和日本理化學研究所(RIKEN)、東京大學學者,及美國哈佛大學學者合作,發現拓撲半金屬在太赫茲電磁輻射下會產生龐大的體光伏效應,其產生的四種光電流完全取決於電子態的微分幾何量[1]。
上述成果發表後,他們進一步將光學躍遷矩陣元素對應固體布洛赫電子態空間之流形體的切向量,並引進黎曼度量張量、度量連接和曲率,建構了一套任意階物質光學響應的黎曼幾何理論,且預言部分量子材料中,三階光伏霍爾效應由黎曼曲率張量主導[2]。這兩項開創性研究成果分別發表於物理學頂尖期刊《物理評論X》和《自然物理》。
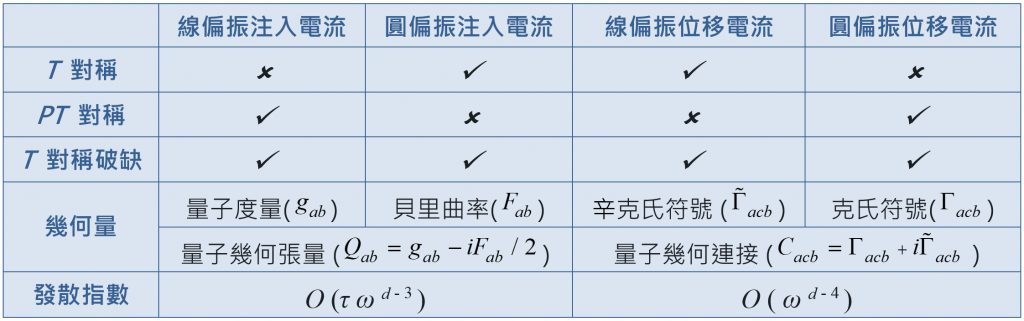
表1. 空間反轉(P)對稱破缺的拓撲半金屬的體光伏效應種類、對應的微分幾何量及光電流的發散程度[1]。T:時間反演,ω:入射光頻率,d:空間維度,τ:載子馳逸時間。
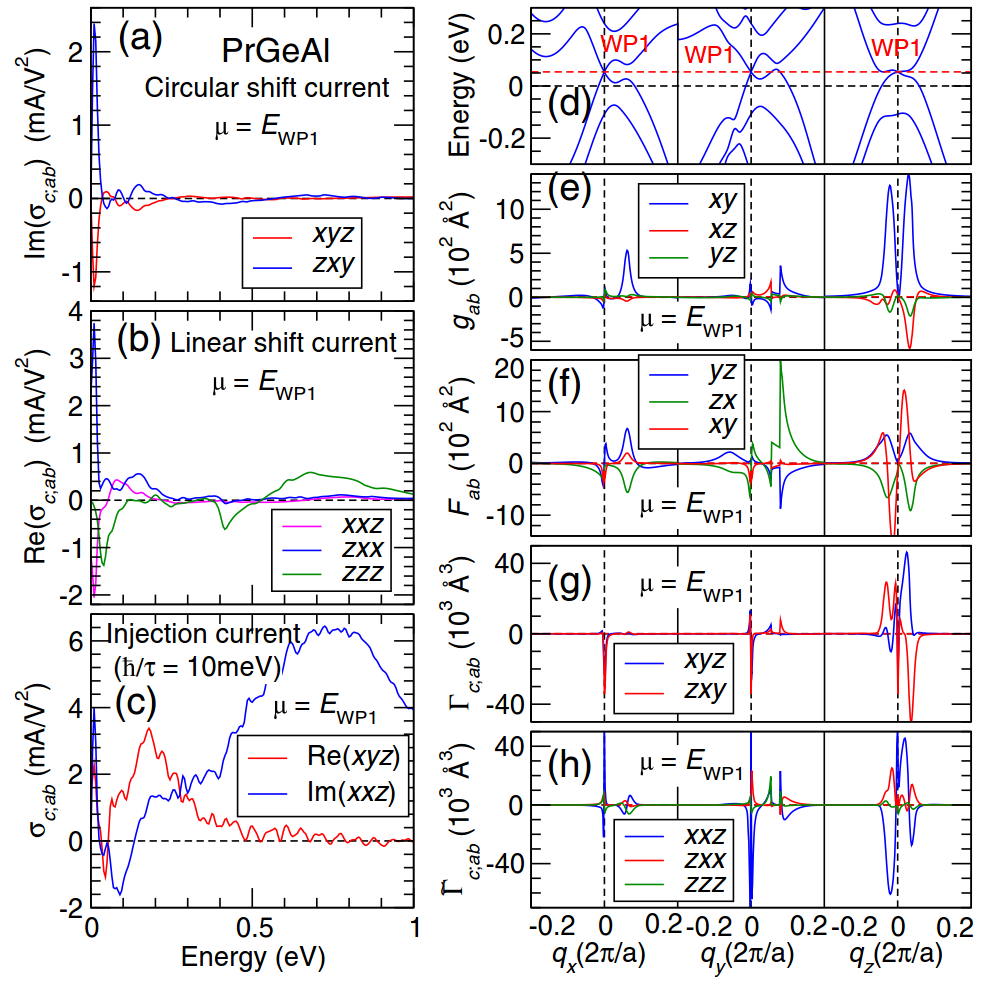
圖1. 鐵磁維爾半金屬鐠鍺化鋁(PrGeAl)的(a)圓偏振和(b)線偏振位移電流電導及(c)圓偏振和線偏振注入電流電導,(d)維爾節點附近的電子能帶,(e-h)微分幾何量[(e)量子度量,(f)貝里曲率,(g)克氏符號及(h)辛克氏符號][1]。
拓撲半金屬的體光伏效應,與電子態微分幾何量的關聯性
體光伏效應屬於物質二階非線性光學響應的一種,指空間反轉(P)對稱破缺的材料,在光照下產生直流光電流的效應。由於體光伏效應在光伏太陽能電池和第六代(G6)手機通信技術皆有應用前景,因此引起人們高度關注。
2020年,郭教授訪問RIKEN新興物質科學研究中心,合作研究固體的二階非線性光學特性。他們先應用指數計算和對稱性分折,探討用來描述維爾和狄拉克半金屬的二個狀態的維爾粒子模型及二個雙重簡並狀態的狄拉克粒子模型二者的體光伏效應,找到光電流隨光頻率趨近零時的發散指數(表1),並發現拓撲半金屬在低頻(如太赫茲)電磁輻射下皆會產生龐大的體光伏效應。
體光伏效應產生的四種光電流完全取決於材料對稱性,其大小由費米能階附近電子態的微分幾何量決定(表1)。P和T皆不對稱,但有PT對稱性的狄拉克半金屬,如三氧化錳鍺(MnGeO3),僅會產生線偏振注入電流和圓偏振位移電流(表1),且幾何量分別由狄拉克節點附近的克氏符號和量子度量決定。
為驗證理想維爾和狄拉克粒子模型的新穎預測的可靠性,郭教授與RIKEN研究者應用第一原理密度泛函理論,計算真實鐵磁維爾半金屬鐠鍺化鋁(PrGeAl)的光電導、量子幾何量,及維爾節點附近的能帶(圖1)。結果說明(1)太赫茲光照射拓撲半金屬產生的巨大光電流,源於材料量子波函數的幾何特性,與(2)體光伏效應是探討物質電子態量子幾何結構的重要工具。
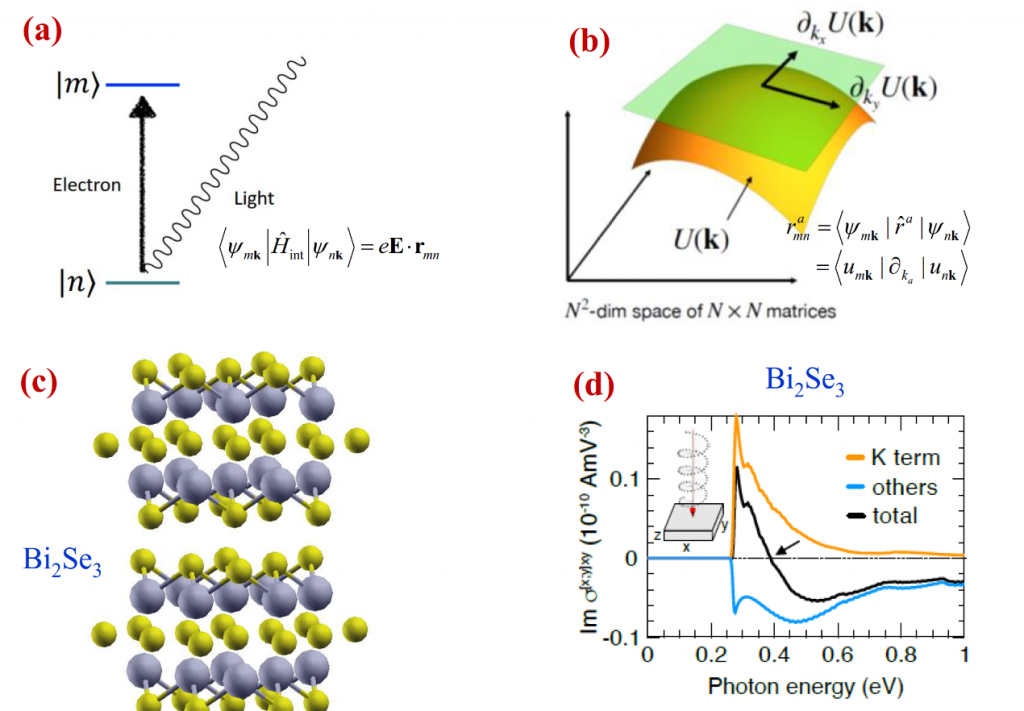
圖2. 任意階物質非線性光學響應的黎曼幾何理論與實驗圖。(a)光激發電子躍遷矩陣元。(b)固體布洛赫電子態空間之流形體的切向量。(c)三硒化二鉍(Bi2Se3)晶軆結構。(d)三階圓偏振光伏霍爾效應的光電導,在吸收帶附近,光電導能譜主要來自黎曼曲率的貢獻(K term)。
建立任意階物質非線性光學響應的黎曼幾何理論
量子幾何是理解電子系統對靜態電磁場響應的基礎。然而,如何將量子幾何與光學響應作聯接則具挑戰性,困難在於光激發的電子躍遷涉及一對狀態[圖2(a)],而已知幾何量(如貝里曲率)僅為單一狀態定義的[1]。迄今為止,光學響應的幾何理解僅限於兩個狀態的系統如前面提到的維爾和狄拉克粒子模型[1],因為兩個狀態的希爾伯特空間完全由單一狀態決定的。
郭教授與合作學者發現,固體布洛赫電子態的動量空間可以看作黎曼空間[2],而且電偶極矩光學躍遷矩陣元可以看作黎曼空間之流形體的切向量(圖2b),他們引進相關的微分幾何量如黎曼度量張量、黎曼度量連接和黎曼曲率,為量子材料的任意高階光學響應建構了一套黎曼幾何理論,這顯示抽象的微分幾何量能決定可量測物質的光學響應物理量。除了描述微分幾何量、體光伏效應和物理量的關聯性外,他們預言三階光伏霍爾效應是由黎曼曲率張量主導,並提出驗證此預言的實驗(圖2c、d)。此成果發表於物理學頂尖期刊《自然物理》。
參考文獻
[1] J. Ahn, G.-Y. Guo, and Naoto Nagaosa, Low-frequency divergence and quantum geometry of the bulk photovoltaic effect in topological semimetals, Phys. Rev. X 18, 041041 (2020).
[2] J. Ahn, G.-Y. Guo, Naoto Nagaosa and A. Vishwanath, Riemannian geometry of resonant optical responses, Nat. Physics 18, 290 (2022).