撰稿 / 張鳳吟 (科學推展中心特約編輯)
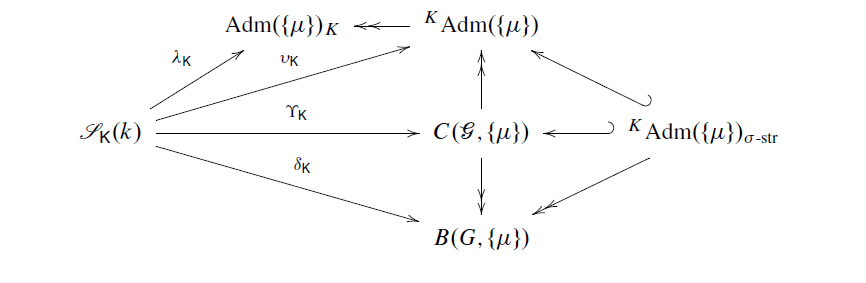
圖1、猜想的EKOR交換圖表(commutative diagram)。
模曲線(modular curve)和模型式(modular form)在整個數學發展扮演極重要的角色,從19世紀以來,就一直是數論學家最關心的主題。模型式是複數上半平面一種具高度對稱的特殊解析函數,在1955年,日本數學家志村五郎與谷山豐提出他們的谷山―志村猜想(Taniyama-Shimura Conjecture),說明每個橢圓曲線(代數幾何裡的對象)都具有一個模型式,這個猜想後來成為英國數學家Andrew Wiles證明著名的費馬最後定理的關鍵。
模曲線指該曲線可用模函數參數化,志村五郎於1960年代提出的志村簇(Shimura varieties)可視為模曲線在高維時的類比。代數幾何中,由多項式方程的解之集合所形成的空間稱為代數簇,是代數幾何主要的研究對象。志村簇是一種特殊的代數簇,在代數幾何有著極為重要的地位,它與許多重要的課題,如模空間、Galois表示、自守形式(automorphic form)等息息相關,並是稱為數學大統一理論的Langlands綱領中最核心關鍵的研究領域之一。中研院數學所研究員余家富博士長期致力於志村簇算術與幾何性質的研究,擁有多項代表性著作,優異的成績讓余家富博士在去年2021年榮獲科技部傑出研究獎及中華民國數學會學術獎。
余家富博士對於志村簇對質數p簡化(reduction modulo p)的幾何很有興趣,他是這方面的專家。志村簇模p有豐富且複雜的結構,代數幾何的基本問題涉及到對子代數簇的分類:1994年,Ekedahl與Oort在優化(good reduction)的情況下 ,提出了 EO 細分(stratification),目的是用來研究牛頓細分;Kotlwitz和Rapoport在Iwahori階結構(level structure)模空間裡,提出KR細分的初步想法,其幾何結果在2008年由余博士與 U. Gortz獲得。2016年,數學家何旭華與Rapoport構想了一個新分類方法,稱為EKOR細分(Ekedahl-Kottwitz-Oort-Rapoport stratification),結合上述兩種細分方法,尋求在parahoric階結構志村簇上的細分,使得它在優化情況成為EO細分,而在Iwahori階結構情況為KR細分。余家富博士與合作者以不同設定,在Kisin與Pappas近期提出的志村簇整模型(integral models)的基礎上,成功以幾何方式建構了EKOR細分(圖1為EKOR交換圖表),並證明它的子流形(EKOR strata)的幾何性質包括光滑性、維度,以及包含關係(closure relation),此成果發表於世界頂尖的期刊《杜克數學期刊》上[1],備受矚目。
余家富博士另一個代表性工作是研究三維超奇異阿貝爾簇(supersingular Abelian varieties)的算術性質[2]。超特殊阿貝爾簇(superspecial Abelian varieties)與四元數格(quaternion lattices)之間有自然的對應關係,由於在四元數格上可定義所謂的質量公式,而超特殊阿貝爾簇為超奇異阿貝爾簇之特殊情形,人們會進一步想問超奇異軌跡(supersingular locus)點上的質量計算問題。1987年,Katsura與Oort以類數(class number)對三維的Siegel模簇(阿貝爾簇模空間)的超奇異軌跡做出明確描述。余博士研究團隊在新的研究中,運用模空間每個點的質量,引入一種稱為質量細分(mass stratification)的分類方法。主要結果給予質量細分一個清楚的描述,並計算出每一個質量子流型上的質量公式,團隊證明,對每個奇質數,都存在11個質量子流型。質量細分內含了超奇異阿貝爾簇豐富的算術性質,如自同態群(automorphism groups)及自同態環(endomorphism rings),透過精細的質量公式,團隊研究三維超奇異阿貝爾簇的自同態群,進而得到三維超奇異阿貝爾簇上Oort猜想的證明,這是Oort猜想21年來最新的突破。
在自守形式方面,余家富博士新的研究源自法國數學家J. P. Serre於1987年寫給美國數學家J. Tate關於模p模型式的信,而Serre的結果也被視為是Jacquet-Langlands對應的模p類比。利用代數模型式的理論,余家富博士成功將Serre的Jacquet-Langlands模p對應,從原來的橢圓模曲線,推廣至任意霍奇(Hodge)型的志村簇上[3]。
余家富博士表示,他非常享受和合作者與同事們討論數學、互相學習的過程,並勉勵自己:多想想、多看看、多交流。研究起起伏伏很正常,多運動保持平常心,長期下來自然會看到不少研究成果。
參考文獻
[1] Xu Shen, Chia-Fu Yu, Chao Zhang EKOR strata for Shimura varieties with parahoric level structure, Duke Mathematical Journal, 170 (2021) no. 14, 3111-3236.
[2] Valentijn Karemaker, Fuetaro Yobuko and Chia-Fu Yu, Mass formula and Oort’s conjecture for supersingular abelian threefolds. Adv. Math., 386 (2021), 107812, 52 pp.
[3] Yasuhiro Terakado and Chia-Fu Yu, Hecke eigensystems of automorphic forms (mod p) of Hodge type and algebraic modular forms, Math Ann. 382 (2022) no. 1-2, 69-102.