撰稿 / 陳宣豪 (科學推展中心特約編輯)
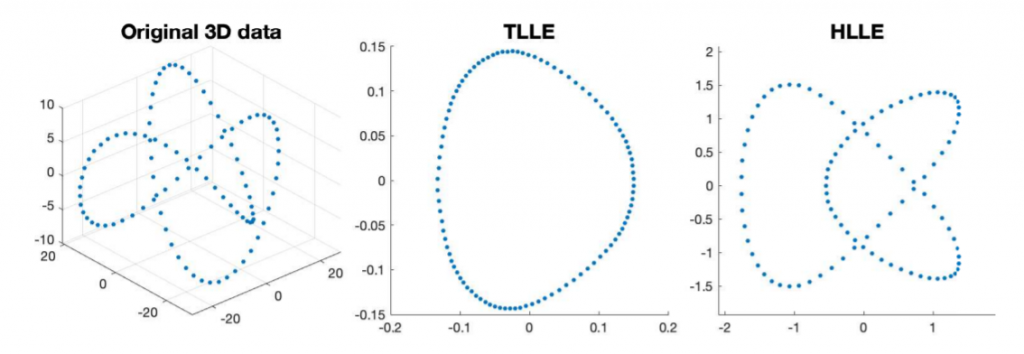
圖1. Original 3D data、TLLE、HLLE之比較
由於資料儲取、運算速度、數據流通等因素的提升,全球開啟大數據(big data)浪潮,可謂近年顯學,然而大數據在數面向已與傳統數據截然不同,需要新的方法與思維來處理,例如過往受限計算方面的技術困難,許多問題只能抽樣處理,如今可直接分析母群體。不過這樣的進步,同時讓資料更為混雜(hybridity),包括資料維度、缺失、乾淨程度、類別等,以及這些數據也沒有明確的標籤(label),即哪些變數可作為自變數、哪些可作為應變數來分析等,而非監督式學習(unsupervised learning)則適合處理這樣的挑戰。
因此巨大資料量、資料混雜、數據無標籤等面向差異,讓現今數據科學家無法直接從統計數據或圖表來掌握全貌,必須使用更多降維(dimensionality reduction)的方式來處理,例如低維嵌入(low-dimension embedding)。其次也需要更加穩健的嵌入演算法,和數學理論來確保機器能自行發現重要的統計特徵(feature)。
其中,流形學習(manifold learning)正是為了解決上述問題而誕生的領域,龐大的數據是以數位化方式儲存於高維歐氏空間,而數據可能會依某些特定的結構分佈,並非隨機散佈在高維空間,因此可以合理假設當資料點在沒有雜訊(noise)的情況下會分佈在一個低維子流形(submanifold)裡。所以流形學習的目標就是讓機器有能力學習(learn)這個子流形,例如使用幾何、非線性、非監督式的統計學習方法,而中山大學應用數學系陳志偉助理教授便專注於研究「資料之非線性低維嵌入」,且將其收斂性、降噪、度量設計等都納入考慮。
常見低維嵌入法有主成分分析(PCA)、多維標度法(MDS),而新近流形學習法有等距映射(Isomap)、局部線性嵌入(LLE)、黑森局部線性嵌入(Hessian LLE)、拉普拉斯特徵映射(Laplacian Eigenmap)、擴散映射(Diffusion Map)、t分布隨機鄰域嵌入(t-SNE),這些嵌入法都已廣泛應用於各領域。可惜的是,這些嵌入法多數未取得充足的理論證明。目前已有許多實務問題必須要從理論上來處理,若能將數據科學堅實地建立在數學理論上,勢必將能把技術提升到另一層次,並為操作過程出現的問題提供解釋。
現今被數據科學家最重視地則是「一致性問題(consistency problem)」:把高維空間裡子流形上的n個數據點嵌入低維空間後,若數據點愈取愈密(在某個意義下讓n趨於無窮大),嵌入法是否收斂?何時收斂?這些都會影響嵌入法的穩定、誤差以及判斷準確度。
目前陳志偉助理教授已與美國杜克大學數學系暨統計系吳浩榳教授合作,找到在離散資料點上定義黑森(Hessian)矩陣的方式,並證明當數據點愈取愈密時,矩陣會收斂到連續的黑森矩陣,解決了一般資料於流形上的離散黑森矩陣之定義問題,並為黑森局部線性嵌入提供了一個理論基礎。該研究是透過設計一個最佳化問題並定義其解為函數f的離散黑森矩陣,再計算它與連續黑森矩陣Ddf的差,最後證明此誤差會隨著資料點的增加與估計範圍的縮小而趨近於零。此外,陳教授與林立人博士也設計了一個TLLE演算法,用來改善黑森局部線性嵌入的不足之處。
除了這次理論的驗證,未來研究團隊也將繼續致力於探討整體黑森能量(total Hessian energy)的極小值問題,預期透過對雙拉普拉斯算子(bi-Laplacian)的研究來掌握其特徵函數的嵌入性質。