撰稿 / 張鳳吟 (科學推展中心特約編輯)
克羅內克極限公式(Kronecker limit formula)是德國數學家利奧波德•克羅內克(Leopold Kronecker,1823-1891)在他關於橢圓函數的書中,提出用來應用於各式算數問題的極限公式。自1863年提出後,克羅內克極限公式便被大量研究,也啟發了後代數學家們的靈感。在近40年,大家開始專注於古典克羅內克極限公式的廣義化及其在數論、幾何與物理上的應用。清華大學數學系魏福村副教授研究總函數體(global function fields) 的克羅內克極限公式,從而廣義化至任意維度的克羅內克極限公式,其優異成果發表於數學界極負盛名的《Inventiones Mathematicae》期刊[1],該論文也獲得2020年世界華人數學聯盟年會「最佳論文銀牌獎」。
古典克羅內克極限公式在一維、二維的例子
故事從黎曼zeta函數\(ζ(s)\)開始。黎曼zeta函數定義為\(\zeta\left(s\right)=\sum_{n=1}^{\infty}\)1/\({n^s}\),其中s為複數,實部Re(s)大於1。黎曼zeta函數在s=1有個單純極點(simple pole),若在s=1附近以洛朗(Laurant)級數展開,黎曼zeta函數可表示成:
\(\zeta\left(s\right)=\frac{1}{s-1}+\gamma+\cdots\)
其中\(γ\)為著名的尤拉常數。由於我們對尤拉常數的理解還是相當有限,因此考慮伽瑪(gamma)函數\(\Gamma(s)\) 在s=1的泰勒展開:
\(\Gamma\left(s\right)=1-\gamma\left(s-1\right)+\cdots\)
從黎曼zeta函數的函數方程
\(\pi^{-\frac{s}{2}}\Gamma\left(\frac{s}{2}\right)\zeta\left(s\right)=\xi\left(s\right)=\xi\left(1-s\right)\)
可以得到\(\frac{\zeta^\prime\left(0\right)}{\zeta\left(0\right)}=\ln\) (2π) 的結果,這給予zeta函數在s=0的對數微分值一個幾何的解釋:單位圓周長的對數。這是利用黎曼zeta函數的一維例子,對應高維度出現的類似現象,便是克羅內克極限公式。
在二維的複數平面,將黎曼zeta函數推廣至所謂的艾森斯坦(Eisenstein)級數
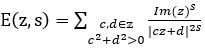
其中複數點\(z\in\mathbb{C}\)的虛部Im(z)大於1。古典的克羅內克極限公式便為艾森斯坦級數在s=1附近展開的常數項。類似上述一維的例子,從艾森斯坦級數的函數方程,我們可以將古典克羅內克極限公式寫成\(\frac{E^\prime\left(z,0\right)}{E\left(z,0\right)}=ln\)(\(Im(z)\)│\(∆(z)\)│\(^{1/6}\)),其中∆(z)為模判別式函數(modular discriminant function),而這公式可視為一維現象在二維空間中的表現,亦即\(E\left(z,s\right)\)在s=0的對數微分值等於單位橢圓曲線(其模判別式的值為1)的面積取對數。
函數體上克羅內克極限公式
由於在更高維度並沒有好的複數結構存在,因此很難將上述例子擴展至2維以上,目前已知有華盛頓州立大學劉昇吉教授在全實體上的結果[2]。為此,魏福村教授提出在德林費週期區間(Drinfeld period domain)總函數體上的克羅內克極限公式。德林費週期區間提供函數體在高維較好的幾何結構,讓我們得以在總函數體研究任意維度的克羅內克極限公式。
體(field)是一種集合,在這集合中可對非零元素進行加減乘除運算。給定有限體\(\mathbb{F}\)的個數為q,定義\(A=\mathbb{F}[t]\) ( \(\mathbb{F}\)的單變數t多項式環)、\(K=\mathbb{F}(t)\) (A的有理函數體)、\(K_\infty{=}\mathbb{F}((t^{-1}))\) ( \(\mathbb{F}\)的單變數\(t^{-1}\)洛朗級數體),並令\(\mathbb{C}_\infty\)為\(K_\infty\)的代數封閉完備化,我們可以將(A,K, \(K_\infty\), \(\mathbb{C}_\infty\))視為古典(整數環\(\mathbb{Z}\)、有理數體\(\mathbb{Q}\)、實數體\(\mathbb{R}\)、複數體\(\mathbb{C}\) )在正特徵值世界的類比。由此,魏福村教授推導出正特徵值上的克羅內克極限公式:
\(\frac{\mathbb{E}\prime(z,0)}{\mathbb{E}\left(z,0\right)}=ln\)(\(Im(z)\)│\(∆(z)\)│\(_{∞}^{\frac{r}{q^r-1}}\))
其中∆(z)為任意秩\(r\)德林費週期區間上的德林費判別式,艾森斯坦級數\(\mathbb{E}\left(z,s\right)\)在s=0的對數微分值便與單位德林費模(Drinfeld module)的體積取對數相關。
魏福村教授表示,透過與古典的類比,正特徵值世界可以發展許多平行於古典數論的理論,甚至利用函數體與幾何的關係看到更多的現象,亦可回頭用更高的觀點試圖解決古典數論中無法突破的問題。利用正特徵值高維度的結果,可以觀察到許多古典裡看不到的現象,例如可考慮四維艾森斯坦級數與格林函數(Green’s function)的關係,藉由導出的克羅內克極限公式來連結L-函數和幾何上相交點個數(intersection number)的關係,並探討正特徵值上高維度的庫德拉(Kudla)綱領,這是魏教授未來研究發展的主要方向。
參考文獻
[1] Fu-Tsun Wei, On Kronecker terms over global function fields, Inventiones mathematicae 220 (2020) 847-907.
[2] Liu, SC. & Masri, R., A Kronecker limit formula for totally real fields and arithmetic applications, Res. number theory (2015) 1: 8.