撰稿 / 張鳳吟 (科學推展中心特約編輯)
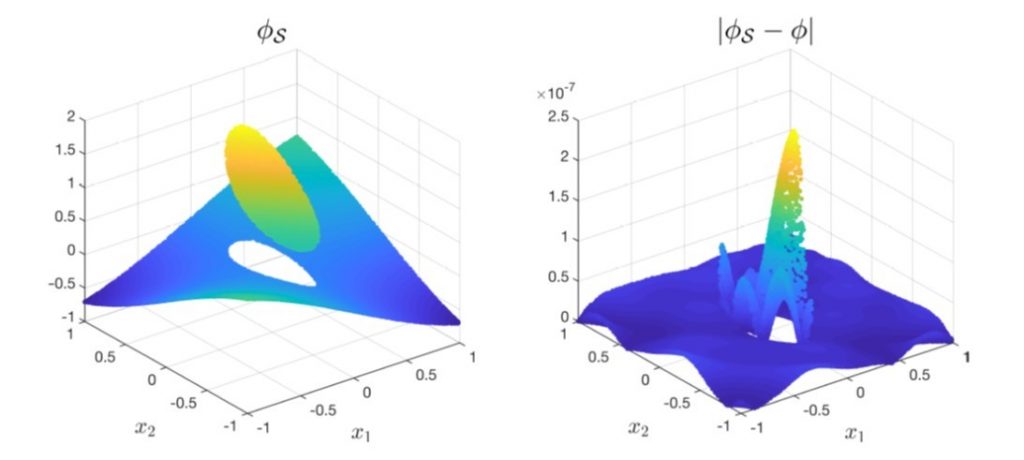
圖1. 左:2維橢圓界面的不連續捕獲淺層神經網路(DCSNN)解,右:DCSNN與正確解的誤差絕對值。
過去十年,深度學習已在影像辨識、自然語言處理、電腦視覺、及其它日常實際應用中取得重大的成功。深度學習是機械學習的分支,是以人工神經網路為架構,對資料進行特徵學習的演算法,而神經網路是一種模仿生物神經網路結構和功能的數學模型。一直到非常近期,科學計算界才開始使用深度神經網路(deep neutral network,DNN)解偏微分方程式(PDEs)的問題。
傳統解PDEs的數值方法包括有限差分、有限元素、或頻譜法,其建立在網格的選取,面對高維度或複雜幾何問題時,計算會變得相當困難。深度學習網路因具備函數通用近似理論與無網格架構限制特性,其優勢使得這類計算變得可行,而廣為流行。一般深度學習網路解PDEs大致分為兩種方法:物理訊息神經網路(physics-informed neural networks,PINN)與深度Ritz方法。前者引進函數近似並透過最小化損失函數(方程式、初始與邊界條件差的均方誤差損失(mean squared error loss))來進行訓練。深度學習在處理PDEs平滑解時相當成功,但較少處理非平滑解或分段(piecewise)平滑解的問題,其中一個典型的範例是橢圓界面問題,它的解與其導數在界面上有跳躍的不連續性。主要困難處是一般神經元所用的激勵函數(activation function)為平滑(如sigmoid函數)或至少是連續的(如ReLU函數)。
到目前為止,深度神經網路在橢圓界面問題最成功的方法學為2020年C. He等人所提出的分段深度神經網路,他們利用對應兩個不相交子域的兩個神經網路,透過解與導數跳躍條件的均方誤差損失連結在一起,利用這方式,訓練出來的解誤差明顯減低,然而,當網路變得更深時,其訓練過程要花更多努力,如同大部分的深度神經網路,可以想見,每一個子域都得訓練個別的神經網路。為此,中央大學數學系胡偉帆副教授與陽明交通大學應用數學系賴明治終身講座教授、林德勝副教授合作,巧妙地發展出一套新的「不連續捕獲淺層神經網路」(discontinuity capturing shallow neural network,DCSNN)來解橢圓界面問題[1]。它有三個新穎之處:(1)可捕捉突然跳躍的不連續;(2)完全淺層,只需要一個隱藏層,大大減低訓練過程的花費;(3)完全無網格,可應用在更複雜區域,特別是高維度問題。新的模型成功應用在近似d維分段連續函數(piecewise continuous function)及更精確求解高維度橢圓界面問題。
不連續捕獲淺層神經網路(DCSNN)
不連續捕獲淺層神經網路(DCSNN)的關鍵想法是,將d維不連續函數擴增(augment)一個座標變數z表示成d+1維的平滑函數,再以淺層神經網路近似這個擴增函數(augmented function)。圖2為闡述這想法的一維例子:其中\(\phi^-\left(x\right)=\sin{\left(2\pi x\right)},x\in[0,\frac{1}{2}]\),及\(\phi^+\left(x\right)=\cos{\left(2\pi x\right)},x\in(\frac{1}{2},1]\),跳躍的不連續發生在\(x=\frac{1}{2}\),如圖2(a)。增加座標變數z,二維的擴增函數可表示為\(\phi_{aug}\left(x,z\right)={\frac{1-z}{2}\phi}^-\left(x\right)+{\frac{1+z}{2}\phi}^+\left(x\right)\),如圖2(b),當z=1相對應於\(\phi^+\left(x\right)\),而z=-1相對應於\(\phi^-\left(x\right)\)。
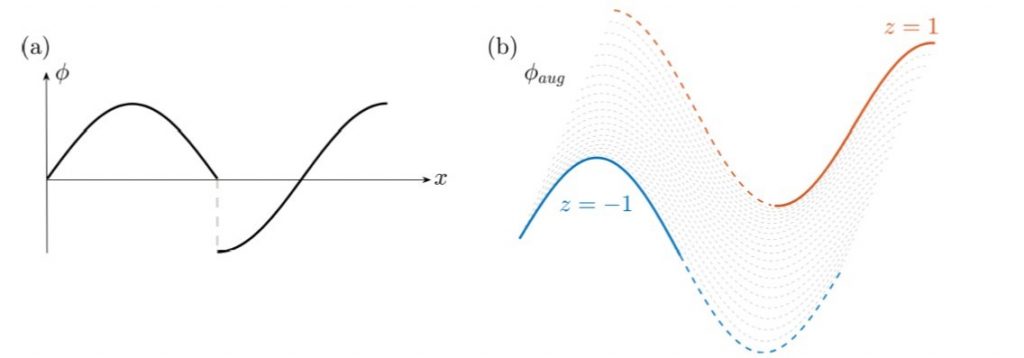
圖2. (a)一維分段連續函數\(\phi\left(x\right)\),(b)不同z值的二維擴增函數\(\phi_{aug}\left(x,z\right)\)。
下一步是建構神經網路來近似d+1維的擴增函數。標準淺層神經網路架構包含輸入層、隱藏層(hidden layer)及輸出層。隱藏層由數個神經元組成,將輸入值給予權重(weight),加上偏差(bias),再經過一個非線性的激勵函數決定神經元的輸出。接著定義損失函數(loss function)比較與正確答案的誤差,透過最小化損失函數來調整參數(權重、偏差)進行學習與訓練。圖3(a)為DCSNN的結構,輸入層加入擴增變數z,損失函數定義為\(\phi\left(\mathbf{x}^i\right)\)輸出與擴增函數\(\phi_{aug}(\mathrm{x}^i,z^i;\mathbf{p})\)的誤差平方平均:
\(Loss\left(\mathbf{p}\right)=\frac{1}{M}\sum_{i=1}^{M}{(\phi\left(\mathbf{x}^i\right)-\phi_{aug}(\mathbf{x}^i,z^i;\mathbf{p}))}^2\)
其中p為訓練參數(權重、偏差)集合的向量,M為訓練的資料數。圖3(b)為圖2 一維範例的結果,實線為分段連續函數\(\phi\),點為DCSNN模型的訓練結果\(\phi_S\)。
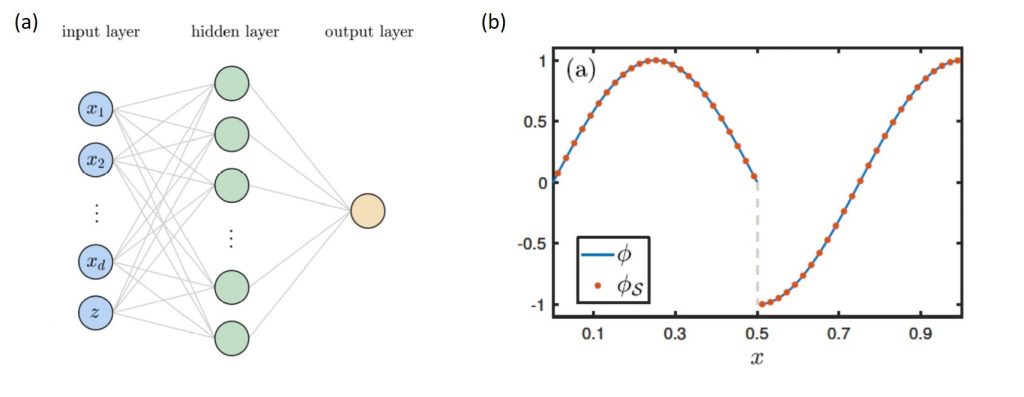
圖3. (a) DCSNN架構,(b) 一維分段連續函數的近似結果,實線為分段連續函數\(\phi\),點為DCSNN模型的訓練結果\(\phi_S\)。
橢圓界面問題
接下來應用DCSNN來解d維變數係數橢圓界面的問題。橢圓界面問題經常出現在流體與材料的計算,起因為材料界面上物理特性的不連續。一般橢圓界面問題方程式如下:
\(\nabla\cdot\left(\beta\left(\mathbf{x}\right)\nabla\phi\left(\mathbf{x}\right)\right)=f\left(\mathbf{x}\right)\),\(\mathbf{x}\in\Omega\)\\(\Gamma\),\(\left[\phi\right]_\Gamma=v\),\(\left[\beta\partial_n\phi\right]_\Gamma=w\)
其中\(\beta\left(x\right)\)是變數係數,\(\Omega\)是歐式空間中一個區域,被界面\(\Gamma\)分割成數個不相交的子區域。框框\(\left[\cdot\right]_\Gamma\)代表在界面上的跳躍不連續。胡偉帆教授團隊考慮簡單的例子,定義界面內\(\beta\left(\mathbf{x}\right)=\beta^-\)、界面外\(\beta\left(\mathbf{x}\right)=\beta^+\),將方程式簡化成Poisson方程式的形式:
![]()
引進d+1維擴增函數\(\phi_{aug}\left(\mathbf{x},z\right)\)滿足
![]()
如此界面的跳躍條件即可透過z=1與z=-1之間的差來估算,也就是\(\left[\phi_{aug}\right]_\Gamma=\phi_{aug}\left(\mathrm{x},1\right)-\phi_{aug}\left(\mathrm{x},-1\right)\),以此類推。
胡偉帆教授將訓練的點分布在區域內、區域邊界及沿著界面,以PINN架構透過最小化方程式、邊界條件及界面條件差的平均平方差(損失函數)解出方程式。由於只有一層隱藏層與中等數目的訓練參數,DCSNN可以在不失精確度下達到極好的計算效率。圖1為2維的計算結果(界面為橢圓形),使用128個訓練點(64個區域內、32個邊界上、32個界面上), 20個神經元。左圖是DCSNN解的輪廓,可看到DCSNN解可以精準突然捕捉到不連續的部分。右圖為DCSNN與正確解的誤差絕對值(~10−7),誤差集中在界面附近。
胡偉帆教授團隊將結果與現有的分段深度神經網路,以及專用於橢圓界面問題的沉浸界面法(immersed interface method,IIM)做比較,顯示DCSNN有更好的精確度,並且更有效率。團隊更將DCSNN應用在2維、3維、6維的例子,展現它在高維計算的能力。
胡偉帆教授表示,此研究工作目前只考慮了穩定橢圓界面問題,後續的延伸工作將會考慮時間相依問題,特別是移動界面問題。
參考文獻
[1] W-F Hu, T-S Lin and M-C Lai, ‘A discontinuity capturing shallow neural network for elliptic interface problems ‘, ArXiv: 2106.05587