撰稿 / 張鳳吟 (科學推展中心特約編輯)
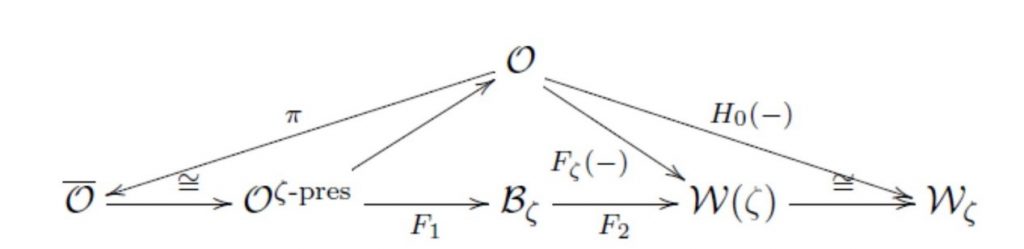
圖1、李超代數 \(\mathfrak{gl}\left(m\middle| n\right)\) 相關模範疇交換圖表。其中\(\overline{\mathcal{O}}\)為BGG範疇\(\mathcal{O}\)的Sere商範疇、\(\mathcal{B}_\zeta\)為Harish-Chandra\(\ \ \left(\mathfrak{g},\mathfrak{g}_0\right)-\)雙模範疇、\(\mathcal{W}(\zeta)\)為Whittaker模範疇、\(\mathcal{W}_\zeta\)為 \(\mathfrak{gl}\left(m\middle| n\right)\) 的主有限W-超代數上模的範疇、F1與F2為Milicic-Soergel等價。
對稱性在大自然中普遍存在,它代表系統經由一個操作,從一個狀態變成另一個等價的狀態,例如,正方形在旋轉90˚度後,和原正方形相等。在數學中,對稱性可由群(group)來描述,它是一種集合加上一種運算組成的代數結構,滿足封閉性、結合性、單位元素與反元素的條件。由於這些代數結構通常很抽象,難以用簡單的方法來描述它們,數學家將群或代數結構化作較具體的矩陣形式,使得原結構的代數運算對應到矩陣的運算,這種表示方式稱為群或代數的表現理論(representation theory)。
李群和李代數是非常重要的代數結構,由於它們對對稱性的描述,在數學和理論物理都有相當重要的地位。李群是個連續變換群,最初由挪威數學家 Sophus Lie創立來處理偏微分方程的連續對稱性,它在單位元素附近的正切空間(無窮小群)為李代數,類似曲面與切面的關係,因此李代數決定了李群的局部性質,並具備向量空間的結構。李代數向量空間g滿足雙線性二元運算[.,.]:g×g→g,以及交錯性與Jacobi恆等式,我們可以定義g上的表現理論,其基本問題是如何找出並刻劃所有不可約表現(irreducible representation)。1925年,數學家嘉當(Gartan)完成了複半單李代數(complex semi-simple Lie algebra)分類,也透過嘉當分解完成複半單李代數有限維不可約表現的分類;印度數學家威瑪(Verna)在他1966年的博士論文中建構出一類半單李代數的無限維表現(現在稱威瑪模)。1980年代,數學家Kazhdan與Lusztig提出著名的Kazhdan-Lusztig理論,計算了BGG範疇O(複半單李代數的一類權模(weight module)模構成的範疇,是李代數表現理論的重要研究對象)的不可約表現的特徵,最終完整回答李代數不可約最高權表現(highest weight representation)的分類問題。
1966年,日本理論物理學家宮沢弘成首度提出超對稱理論(supersymmetry),假設費米子與玻色子之間的對稱,這個理論定義出新的代數結構,稱李超代數(Lie superalgebra),李超代數為李代數的Z2階化推廣。李代數也是一類李超代數,因此可想見其結構之豐富與複雜。1978年左右,Victor Kac首先得到單型李超代數的完整分類,此後人們對幾類的李超代數較感興趣:1、基本型:gl(m|n)、sl(m|n)、psl(n|n)、osp(m|2n);2、基本例外型:D(2|1;α)、F(3|1)、G(3);3、奇特型:p(n)、g(n)。但李超代數的表現理論至今尚未完全建立。李超代數有平行於李代數表現理論中的研究對象,也可定義BGG 範疇 O,但李超代數中的問題都非常困難,主要是因為古典技巧大多無法順利推展到李超代數,它Z2階化的奇部分(odd part)會造成問題,因此沒有一致的理論。近年來李超代數最重大的突破,便是中研院數學所程舜仁研究員、成大數學系林牛教授及維吉尼亞大學數學系王偉強教授共同證明的Brundan-Kazhdan-Lusztig猜想。
國科會111年度吳大猷紀念獎得主,中央大學數學系陳志瑋副教授長期以來致力於李(超)代數的表現理論,特別專注在李超代數不可約的非權表現(non-weight representation)。近期,他與合作者(包括中研院程舜仁研究員及烏普薩拉大學Volodymyr Mazorchuk教授)合作,成功對於李超代數的Whittaker模建立一般理論[1-3]。Whittaker模最初由Konstant引進,他受到Whittaker model的啟發,研究複半單李代數的Whittaker vector及所相應的模。Whittaker模被證明是複半單李代數不可約模分類中重要的一類,E. McDowell、I. D. Milicic、W. Soergel、E. Backelin等數學家為其建立起一般理論,以及它與BGG範疇O之間的關係。
陳教授與合作者研究基本型李超代數(包括gl(m|n))上Whittaker 模及其範疇(categories)[2],他們分類了不可約 Whittaker模、解決了標準Whittaker模的合成因子問題、並得到一個適當的 Whittaker 模範疇。他們也利用 Whittaker模範疇對量子群(Quantum group)以及量子對(Quantum symmetric pair)範疇化。
量子群可以看作q-量子化的李代數,是1986年Drinfeld 和Jimbo在研究楊振寧-Baxter方程時發現的特殊數學結構。陳教授表示,他們的成果可以應用到有限W-代數(finite W-algebra)。有限 W-代數主要起源於1990年代,有許多的主要動機,例如,有限W-代數與仿射W-代數(affine W-algebra)有緊密的關係,而仿射 W-代數可以應用到頂點代數(Vertex operator algebra)或共形場論(Conformal field theory)。圖1為相關的研究對象。
參考文獻
[1] Chih-Whi Chen. “Whittaker modules for classical Lie superalgebras.” Communications in Mathematical Physics 388.1 (2021): 351-383.
[2] Chih-Whi Chen, Shun-Jen Cheng, and Volodymyr Mazorchuk. “Whittaker categories, properly stratified categories and Fock space categorification for Lie superalgebras.” ,arXiv:2203.00541 (2022).
[3] Chih-Whi Chen and Shun-Jen Cheng. “Whittaker categories of quasi-reductive Lie superalgebras and quantum symmetric pairs.” ,arXiv:2208.08778 (2022).