撰稿 / 張鳳吟 (科學推展中心特約編輯)
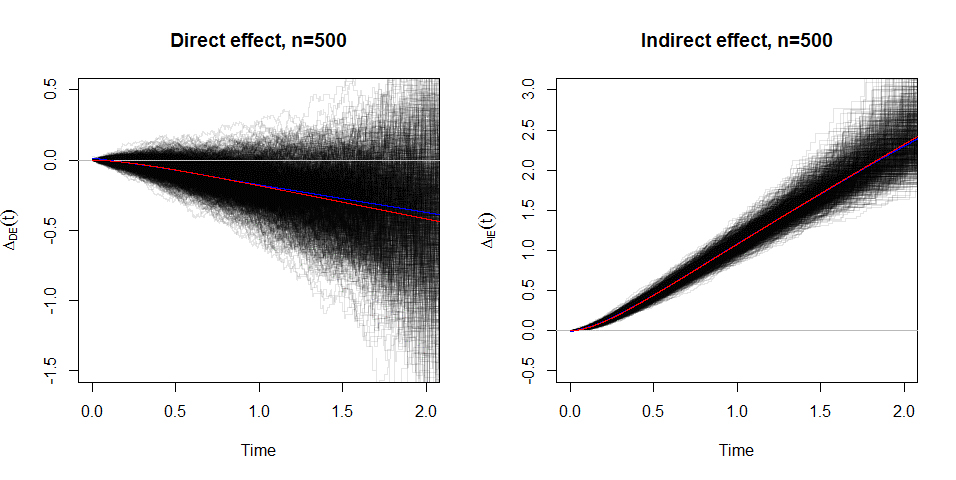
圖1、對立假設(alternative)下數值模擬結果,其中藍線代表移動平均,紅線代表真實的過程。
因果中介模型(causal mediation model)為統計學的新興領域,用來探討何種機制造成事件X與Y之間的因果關係[1],中研院統計所黃彥棕博士結合因果中介模型與醫學統計常用的半競爭風險問題,以因果中介模型為架構來詮釋半競爭風險,提供另一個半競爭風險的分析方式,其優異的成果發表在生物統計頂尖期刊《Biometrics》[2],並編選為當期討論文章[3],廣邀該領域專家評論其研究成果[4-7],受國際矚目。
在醫學實務中,醫師通常會關心病人疾病的預後或存活率的問題,當問題牽涉到追蹤時間的結果時,例如某特殊疾病的5年存活率、10年存活率,或是疾病的復發等,主流的分析方法為存活分析(survival analysis),也是現今被廣泛應用在生物醫學研究上一個統計方式。這方法一般常將病人的追蹤結果分為兩大類:(1) 發生研究興趣事件者(例如:癌症復發)、(2) 沒發生興趣的事件,稱設限樣本(censor),或更口語地說,也可以稱為被蓋牌的樣本。
但病人的追蹤期間,除了發生研究興趣的事件外,也可能會遭遇到其他不同事件(例如:死亡、車禍、手術等),某些事情一旦先發生了,例如車禍死亡、器官切除,導致病人未來不會有機會發生研究的興趣事件,這類事件就稱為競爭風險(competing risks),像是死亡為癌症復發的競爭風險事件。當競爭風險為單向時,例如,死亡則無法死而復生得到癌症,但得癌症仍會發生死亡,則稱為半競爭風險(semi-competing risks)。當時任教於威斯康辛大學J. P. Fine等人在2001年提出了半競爭風險模型。
傳統上競爭風險有興趣的研究事件為單一事件,半競爭風險的興趣事件包括中間事件(例如:得到癌症)與主要事件(例如:死亡),可提供中間過程對於病程的相關訊息。中間事件可能被主要事件設限(或,蓋牌),反之,發生中間事件仍可進程至主要事件。許多人類病史或病程都可被視為半競爭風險的問題,例如病毒性肝炎進展到肝癌到死亡的關係,這也是黃彥棕博士主要的研究動機。
一般半競爭風險的資料研究集中在中間結果與主要結果的聯合存活函數(joint survivor function,存活函數代表事件發生時間大於某時間的機率),一個常用的方式是假設中間結果(時間T1)與主要結果(時間T2)的存活函數遵循關聯結構模型(copula model,處理統計隨機變數關聯性問題);另一種為多狀態模型(multi-state model),將半競爭風險分為三個狀態,包括健康(狀態1)、生病(狀態2)、死亡(狀態3),這方式主要探討狀態之間的轉換機率。雖然這些現有的方式都能表示肝炎狀態轉換的風險,但對考慮因果關係的解釋仍嫌不足,為此,黃彥棕博士引進因果中介模型,想了解B型肝炎直接或間接(經由肝癌)造成死亡的影響,定義半競爭風險估計量的科學解釋。
中介分析(mediation analysis)最早由Baron 與 Kenny於1986年在社會科學文獻中提出[8],中介分析將兩個事件X對Y造成的作用分解成:透過中介因子(mediator)所造成的間接效應(indirect effect)、及不透過中介造成的直接效應(direct effect)。後來1992年美國統計及流行病學家James Robins與Sander Greeland[9],與2001年資訊科學及統計學家Judea Pearl[10]對其做嚴謹的因果推論(causal inference),為統計學與因果推論確立了一門新興領域:因果中介模型。黃彥棕博士將半競爭風險問題放入因果中介模型的框架中:將半競爭風險的中間事件設為中介因子,主要事件設為結果;並定義間接效應(IE, indirect effect)為「X對主要結果(Y)透過中間事件的作用」,而直接效應(DE, direct effect)為「X不經過中間的事件對主要結果(Y)的作用」[3]。在此框架下,提出反事實風險(counterfactual hazard),定義出與中間事件相關的主要結果的直接及間接效應:\(∆_{IE} \)及\(∆_{DE} \),進而提出其非參數的估計式(nonparametric estimators),\(\widehat{∆}_{IE} \)及\(\widehat{∆}_{DE} \) 。
圖 1 為模型估計式效能的數值實驗結果,樣本數為500,前一半暴露(exposures,致病因子)設為1,後一半設為2,資料產生遵循Weibull分佈。數值實驗結果顯示,所提出的估計式即使在不同的時間點,皆能無偏差地估計所定義的直接及間接效應。
黃彥棕博士將模型應用在調查B型肝炎經由肝癌中介對整體死亡的效應,他集中分析4954個男性受試者,年齡在50歲以下,沒有喝酒的習慣。分析顯示B肝病人透過肝癌發生的間接效應增加了死亡的累積發生率(圖2左紅色曲線),或減少存活機率(圖2右紅色曲線);而B型肝炎對死亡的直接效應(沒經過肝癌過程)只有稍微增加累積風險(圖2藍色曲線),不過它的信頼區間也包含了虛無(null)的值。分析結果顯示,在年齡50歲以下的男性,B型肝炎造成死亡的風險主要是透過肝癌。
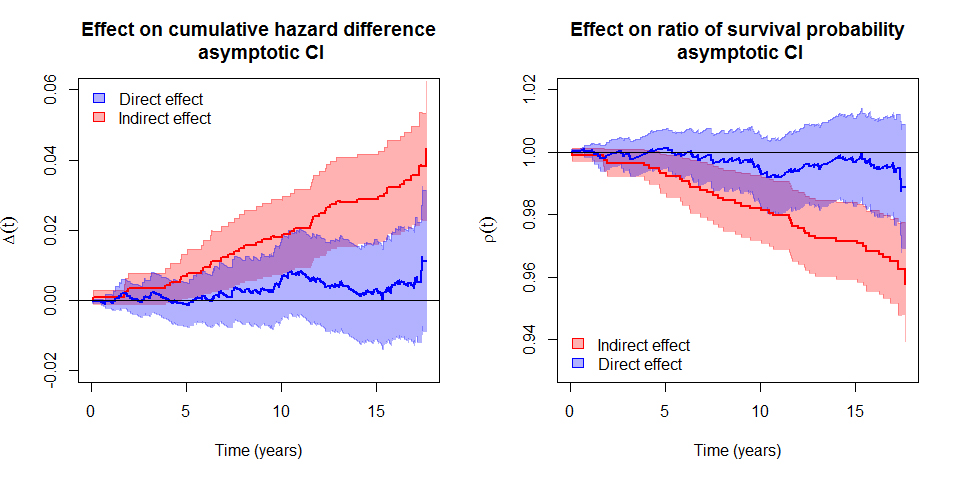
圖2、B型肝炎透過肝癌發生媒介對死亡的直接(不透過肝癌)與間接(透過肝癌)效應。
黃彥棕博士表示,B型肝炎在全世界造成嚴重的公衛負擔,為了減少B型肝炎病人的死亡率,一個可能的辦法是利用抗病毒藥物消滅B型肝炎病毒,但價格昂貴,且有停藥後B肝復發的問題。圖2的分析結果揭示,既然大部份B肝造成的死亡皆透過肝癌,對B型肝炎帶原者進行更積極的肝癌篩檢或許能更有效地減少可預防的死亡。 因果中介模型提供了將暴露介入轉移到中介因子介入來預防結果發生之不一樣的思考。
在此研究中,黃彥棕博士將因果中介模型連結到半競爭風險現有的方法學上,打開後續研究的機會,例如探討多狀態模型中轉變機率與直接和間接效應的關係[7],不僅為現有模型的統計參數提供更好的解釋,也做為統一雙變量存活分析與因果中介分析的關鍵。
參考文獻
[1] 黃彥棕,〈因果中介模型〉,自然科學簡訊第31卷第1期,p24
[2] V Theoharakis and M Skordia, ‘How do statisticians perceive statistics journals?’, The American Statistician (2003), 57, 115-123.
[3] YT Huang, ’Causal mediation of semicompeting risks (with discussion)’, Biometrics (2021), online ahead of print, doi: 10.1111/biom.13525.
[4] KCG Chan, F Gao and F Xia, ’Discussion on “Causal mediation of semicompeting risks”’, Biometrics (2021), online ahead of print, doi: 10.1111/biom.13520.
[5] IR Fulcher, I Shpitser, V Didelez, K Zhou and DO Scharfstein, ’Discussion on “Causal mediation of semicompeting risks”’, Biometrics (2021), online ahead of print, doi: 10.1111/biom.13519.
[6] MJ Stensrud, JG Young and T Martinussen, ’Discussion on “Causal mediation of semicompeting risks”’, Biometrics (2021), online ahead of print, doi: 10.1111/biom.13523.
[7] YT Huang, ‘Rejoinder to “Causal mediation of semicompeting risks”’, Biometrics (2021), online ahead of print, doi: 10.1111/biom.13518.
[8] RM Baron and DA Kenny, ‘The moderator-mediator variable distinction in social psychological research: conceptual, strategic and statistical consideration’, Journal of Personality and Social Psychology (1986), 51, 1173-1182.
[9] JM Robins and S Greenland, ‘Identifiability and exchangeability for direct and indirect effects’ Epidemiology (1992), 3, 143-155.
[10] J Pearl, ‘Direct and indirect effects’ In: Proceedings of the Seventeenth Conference on Uncertainty and Artificial Intelligence. San Francisco, CA: Morgan Kaufmann (2001), 411-420.