撰稿 / 陳宣豪 (科學推展中心特約編輯)
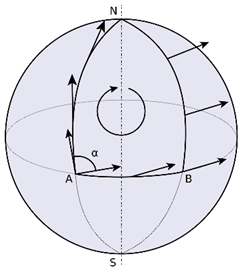
圖1:和樂(holonomy),向量繞行一圈回到起點後會與原先不同。
現代數學眾多流派中,有一主流專注研究微分流形的幾何性質,稱為微分幾何(Differential geometry),其與拓撲學、代數幾何及理論物理之間關係密切。而一個有距離和角度概念的流形(Riemannian manifold,黎曼流形),從一點所對應的空間與另一點所對應的空間之間轉換的和樂(Holonomy,又稱完整)現象,意指向量繞圈平行移動回到起點時會與原先相異,換句話說,在一個流形上讓一個向量沿著一條封閉曲線平行移動一圈,並不一定會回到原本的向量,這樣具有特殊和樂群的流形從古至今便一直是微分幾何主要研究方向之一,而這種沿著一曲線的連續地變化的概念,可以進一步用來研究纖維叢(fiber bundle)的幾何。
現代微分幾何數學研究瓶頸
西元1950年M. Berger曾用代數方式將和樂所有的可能進行分類,不過最後產出是一個清單列表,並無具體成果,而後W. Ambrose和I. Singer發現和樂與流形曲率的連結,接著西元1978年丘成桐(S.-T. Yau)作了重大突破,證明了卡拉比–丘流形(Calabi–Yau manifold)定理,因此後續15年中有越來越多的構造出現,但遲遲未發現一般性的存在定理。

圖2:卡拉比-丘(Calabi-Yau)流形
除此之外,另一關鍵研究課題,便是理解特殊的和樂群的流形之幾何性質,例如研究表面上的最短路徑,或是其中的「肥皂泡面」(Minimal submanifold,極小子流形)。特殊和樂群流形因為結構群的特殊性,自然具備一些平行旋量,因此1982年R. Harvey和B. Lawson發現這些旋量可以用來刻劃極小子流形,並反應出特殊和樂群的幾何性質。而一個構造極小子流形的自然想法,便是沿著體積泛函的梯度反方向去變形子流形,我們稱其為「均曲率流」(mean curvature flow)。
臺大數學系「均曲率流」(mean curvature flow)突破
國立臺灣大學數學系蔡忠潤副教授團隊和王慕道教授一同合作研究特殊和樂群流形,對主要的經典構造進行均曲率流研究,希望藉此瞭解其中的極小子流形,再透過極小子流形來對特殊和樂群有更深刻的認識。事實上,這些幾何物件也在數學物理上扮演重要角色,包含鏡對稱、M理論等。
蔡忠潤副教授指出,這些經典案例中都有其自身的重要性:它們被認為是特殊和樂群在某種極限狀況下的漸進行為。團隊目前已證明這些經典的構造中,其極小子流形具唯一性,亦即所謂的整體剛性;主要突破便是觀察到其幾何的「整體凸性」。在研究團隊突破之前,數學界只知道它們具有局部剛性,但現在進一步發現當中的極小子流形在均曲流之下是穩定狀態,表示在經典例子中使用均曲率流去變形子流形,在一些自然的初始情況下,整個幾何流方程有長時間存在性;並且當時間趨向無限大時,子流形會收斂到極小子流形。蔡忠潤副教授對此表示,這是第一個關於特殊和樂群內均曲流的研究結果。
未來臺灣大學數學系研究團隊將針對結果進一步深入研究,其中一課題是針對有奇異點的特殊和樂群流形研究;另一課題則是應用上述工具,探討一般均曲流的穩定性。團隊期望未來能對這些幾何物件、和它們在幾何流下的行為能有更深刻的發現與瞭解。
參考文獻
[1] 和樂/holonomy
https://zh.wikipedia.org/wiki/%E5%AE%8C%E6%95%B4%E7%BE%A4
[2] 蔡忠潤(2016).研究成果報導:均曲率流.自然科學簡訊,31(4),164-165。https://www.most.gov.tw/most/attachments/a0ceec73-648a-4e57-a0a7-59ae586ff699