中央研究院統計科學研究所 黃信誠
國立清華大學統計所 徐南蓉 周秉儒
前言
空氣品質與健康息息相關,也是重要的民生議題。許多醫學研究都已證實細懸浮微粒(PM2.5)對人體健康的危害,世界衛生組織 WHO也早在 2013 年明訂 PM2.5 為致癌物。臺灣的PM2.5 濃度在地域上有顯著的差異,數值經年是南高北低,並受季風的影響有明顯的季節性。本文聚焦於 PM2.5 極值的時空變異,以台灣高屏地區為例,探究 PM2.5 每日最大值分佈之週期性及時空變化趨勢。我們採用環保署空氣品質監測網之資料(https://www.epa.gov.tw/) [1],以廣義極端值分佈進行統計建模與分析。統計推論的重點有二,其一是以統計方法估計高屏地區 PM2.5 極值分佈之時間與空間(包含無觀測資料地點)變化趨勢;其二是量化「紫爆」( 3 PM2.5 70 μg / m > )發生之機率。
時空極值之建模與分析
廣義極端值分佈(generalized extreme value distribution),簡記為GEV(η ,τ ,ξ ) ,是描述極值資料慣用的機率模型[2],其累積分佈函數如下:
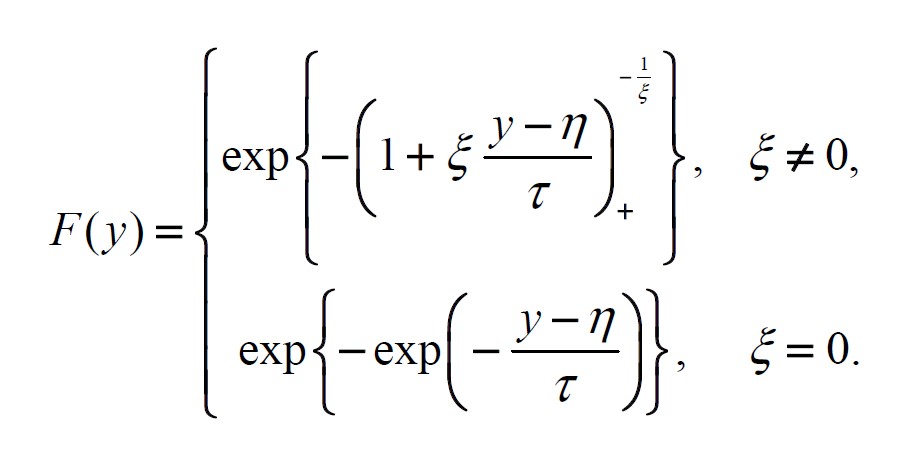
其中,模型的三個參數 (η ,τ ,ξ ) 依序刻畫此分佈之位置(location)、尺度(scale)及其形狀(shape)等特徵。
針對高屏地區 15 個測站 2006-2018 年的每小時長期觀測資料,定義符號:
(1) Si 為 i 測站(i =1, …,15)的地理座標,
(2) Yt (Si ) 為 i 測站在 t 時間(日)PM2.5 的最大日觀測值。
本研究整合該區域所有資料進行時空間分析,假設 PM2.5 在該區域任意地點 s 及任意時間 t 之日極值分佈如下:
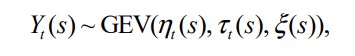
其中 ηt (s), τt (s), ξ (s) 是地理位置 s ∈ R2 (及時間 t ∈ R)的平滑函數。我們藉由平滑基底函數之線性組合建構 ηt (s), τt (s), ξ (s),描述資料在空間之變化與在時間之變動趨勢(包括季節性等)。在時間 t 上採用傅立葉函數及自然樣條函數(natural splines)做為基底函數;在空間 s 上則以多尺度空間樣條函數(multi-resolution spline basi sfunctions) [3]建構空間關係。這樣的模式能有效推導該區域任意地點(包含無觀測資料所在)的極值分佈,在估計上也能適切地利用鄰近區域的資料訊息,提升整體參數估計的準確度。
我們以 2006-2015 年間所有測站的日資料進行分析,採用最大概似(maximum likelihood)估計法進行時空間極值模型配適,並以 2016-2018 年的觀測值檢視推論之成效。
統計推論結果
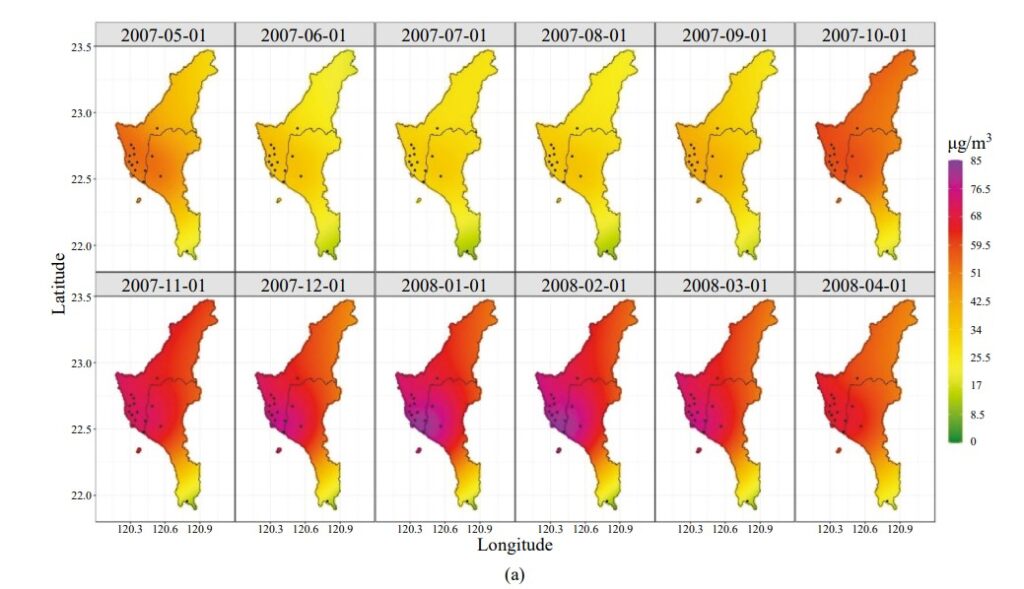
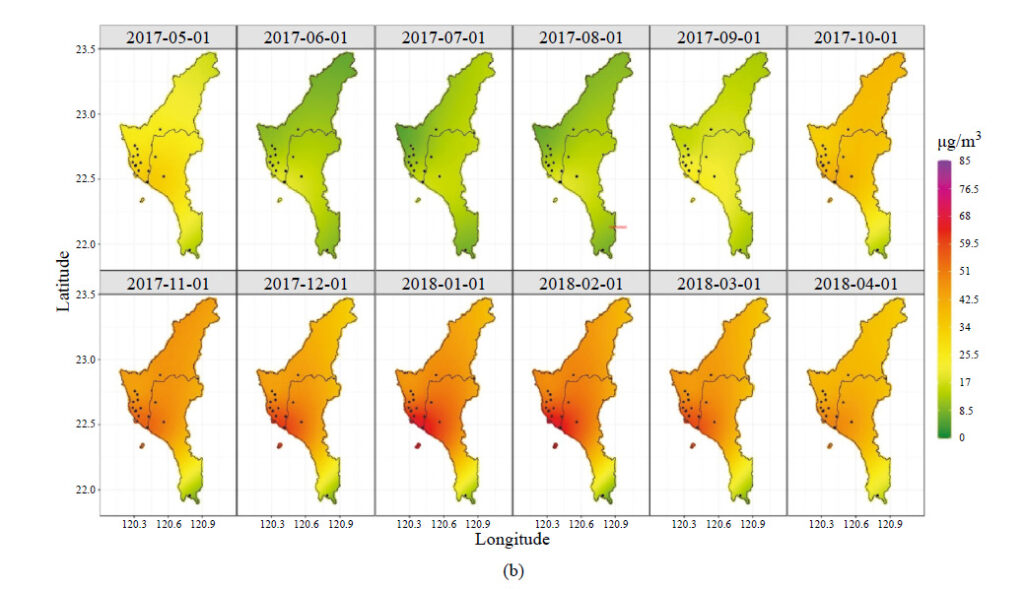
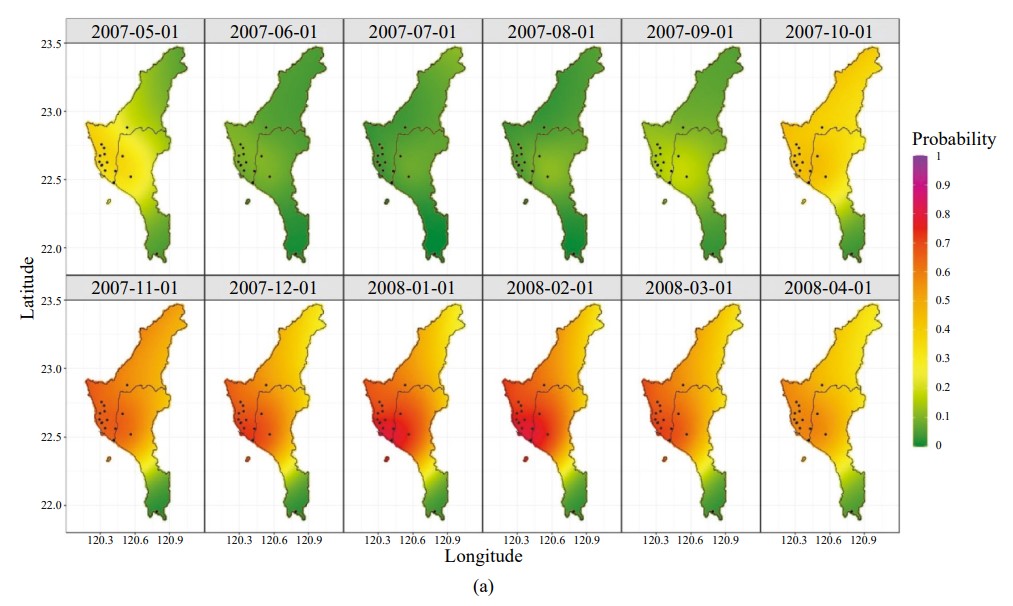
分析結果顯示 PM2.5 的日極值在近十年來已大幅降低,若比較 2007/5-2008/4 與 2017/5-2018/4 兩段時期極值分佈之位置參數 ηt (s) 的變化趨勢(圖一),數值的相對差異清晰可辨,PM2.5 的極值顯著地降低。另受氣候條件的影響,呈現明顯季節週期性,約略可區分為空品較佳的 6-9 月份及空品較差的其他月份(1-5 月及10-12 月)。
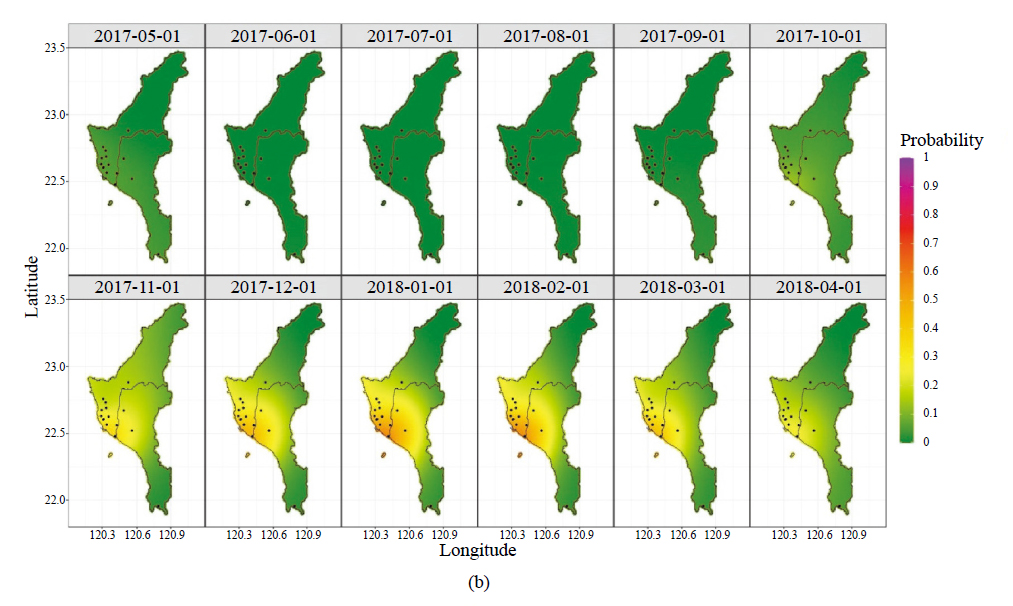
因本研究聚焦於 PM2.5 汙染,故採用環保署在 2016/12 以前對 PM2.5 所定義之紫爆標準( PM2.5 70 μg / m3 > )為門檻(註一),依據配適的時空極值模型估計該區域任意地點之紫爆機率。圖二顯示 PM2.5 的單日紫爆機率在 2007/5-2008/4與 2017/5-2018/4 兩時期的對照,後者發生紫爆的機率明顯降低,改善的幅度在空品較差的季節(1-5 月及 10-12 月)尤其顯著。雖然欣見 PM2.5的極值濃度逐年降低,但目前秋冬之際高雄都會區單日的紫爆機率仍高於 20%,長期曝險對民眾健康的影響需進一步研究。
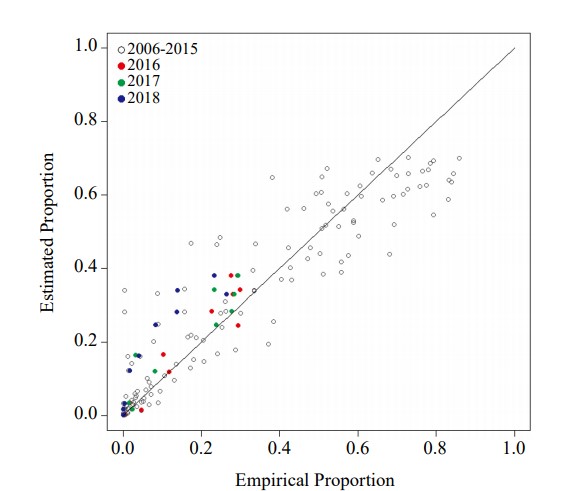
欲確認所建構之時空模型是否適切,我們以每月紫爆發生之比率做為驗證指標,以 2006-2015 年資料所配適之模型,預測 2016-2018 年發生紫爆的比率(以月為單位平均),並與 2016-2018 年實際發生紫爆的比率做比較。圖三顯示模型估計的每月紫爆發生比率(y-axis)與實際紫爆發生比率(x-axis)的散佈圖,並以顏色顯示不同年份的結果,黑色對應訓練資料時期(2006-2015),彩色則對應驗證資料時期(2016-2018)。多數點落在 45 度線的周邊,顯示我們的模型配適良好且確實能有效地推論極值的發生比率。此外,對 2016 年進行領先一年期的預測,紫爆發生比率的估計與實際資料吻合,2017 年次之,2018 年則為領先三年期的預測,紫爆發生比率的估計已明顯高估(藍色點皆在 45 度線之上),再次印證了 PM2.5 的極值近三年仍持續遞減中,與配適模型所用 2006-2015 年資料之極值分佈有顯著差異。
結語
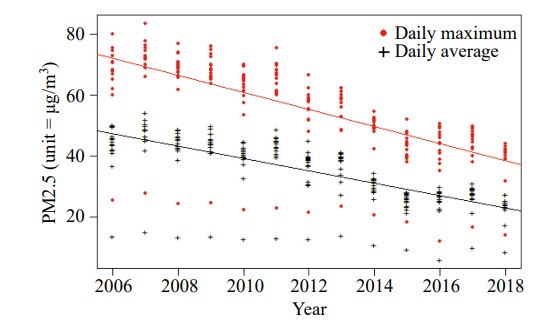
過往對於 PM2.5 的研究,大多探討平均值的長期變化趨勢,統計推估也僅止於測站所在地點,然而受限於 PM2.5 的數值分佈並非對稱,平均值資料訊息較難推估分佈右尾的特徵。以高屏資料為例,圖四顯示高屏地區 PM2.5 日最大值的年均(紅色)與日平均值的年均(黑色)之變化趨勢,其中每個點代表一個測站的年均值,極值的年遞減速率為 2.81 μg/m3(標準誤差 0.20),更勝於平均值的年遞減速率 2.03 μg/m3(標準誤差 0.14)。由於空污議題的重點經常聚焦於PM2.5 大數值的情境,極端值分析更能凸顯這些最糟情況(worst case scenario)的特徵。未來研究將納入空間及時間的相關性結構,輔助研究者進一步了解 PM2.5 極值的動態變化機制,並提供準確即時的預測。
參考文獻
[1] 資料來源:行政院環保署環境資源資料庫,空氣品質監測網(網址:https://erdb.epa.gov.tw/DataRepository/API/API_Description_Page_new.aspx).
[2] Coles, S. An Introduction to Statistical Modeling of Extreme Values, Springer, New York (2001).
[3] Tzeng, S. and Huang, H.-C. Resolution adaptive fixed rank kriging, Technometrics, 60, 198-208 (2018).
備註
[註一] 自 2016 年 12 月起,環保署訂定新的空氣品質指標 AQI,因 AQI 的定義涵蓋多種污染物,依據 AQI 定義之紫爆標準亦不同,詳見環保署網頁。